
|
|
CapVIII-pg4 |
|
O que essas superfícies têm de especial, que as distinga dos outros exemplos que até então mostramos? |
Comecemos tomando a Faixa de Moebius feita de papel e vejamos o que acontece se colocamos uma formiguinha sobre ela (a formiguinha pode ser imaginária, para os alérgicos!). A formiguinha começa a caminhar e dá uma volta completa, mas ao retornar está do "outro lado" do papel. |
É fácil ver que o mesmo pode acontecer nas superfícies A, B e C: há sempre um caminho que a formiguinha pode escolher tal que quando voltar ao ponto de partida ela estará do outro lado do papel. Esse tipo de superfície é chamada de não-orientável, ao passo que as demais são orientáveis. |
Numa superfície orientável como a esfera, por exemplo, se colocarmos duas formiguinhas, uma do "lado de dentro" e outra do "lado de fora", elas nunca se encontrarão. |
Já comentamos, no entanto, que analogias com formigas são um pouco perigosas, pois elas não vivem no mundo bidimensional. Daremos a seguir uma definição de orientabilidade que Aderbal pode verificar, vivendo exclusivamente dentro da superfície. Ele será capaz de dizer se a superfície é ou não é orientável sem precisar conhecer o mundo tridimensional. Veja que não há nenhum sentido, para Aderbal, em se falar dos "lados" de uma superfície. |
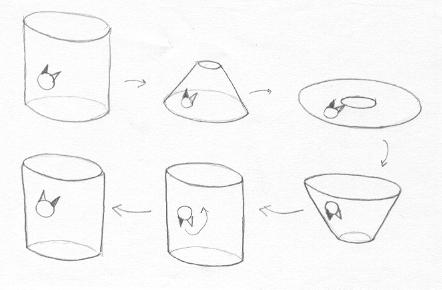
Primeiro vejamos o que acontece com Aderbal quando ele está num mundo orientável: o cilindro, por exemplo. Nesse mundo estão espalhados alguns relógios, que Aderbal gosta de examinar, entrando e vendo o ponteiro girar. |

|
A primeira coisa que Aderbal observa é o sentido do ponteiro. Isso ele faz posicionando-se no centro do relógio e vendo se o ponteiro passa da antena preta para a antena branca ou da antena branca para a antena preta. Para Aderbal não faz sentido falar em "direita" ou "esquerda": no desenho acima, a antena preta está à esquerda para um observador como nós, "externo" ao cilindro, mas está à direita para quem olha "de dentro". Ou senão, podemos inverter o cilindro, e a antena preta passa da "esquerda para a direita". |
|
Entretanto, uma vez que Aderbal está na superfície e o sentido do ponteiro de cada relógio está fixado, ele pode comparar se dois relógios têm ponteiros girando no mesmo sentido, usando as cores de suas antenas. |
Aderbal pode então pedir às autoridades do Mundo Cilíndrico que coloquem todos os ponteiros girando no mesmo sentido. Se da antena branca para a antena preta ou da antena preta para a antena branca não importa, o que interessa é que girem todos no mesmo sentido. A solicitação de Aderbal é sempre prontamente atendida. |
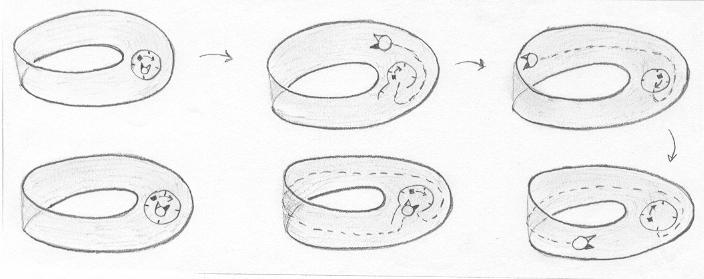
Aderbal às vezes visita a Faixa de Moebius, porém lá, ao contrário do Mundo Cilíndrico, seu pedido nunca é atendido. Felizmente hoje em dia Aderbal já compreende a razão disso. Imagine que ele examine um relógio cujo ponteiro gira, por exemplo, da antena preta para a antena branca, como mostra a figura abaixo. Ele sai para caminhar e dá uma volta completa na Faixa de Moebius. Ao voltar, o ponteiro do relógio está girando ao contrário: da antena branca para a antena preta! |
|
De fato, não há como fazer com que todos os ponteiros girem no mesmo sentido porque não é possível definir um sentido para eles. Isso é o que caracteriza uma superfície não orientável. Já em uma superfície orientável é sempre possível escolher uma orientação para os ponteiros do relógio. |
Esses caminhos que Aderbal percorre e que, ao final, o sentido dos ponteiros do relógio muda, de acordo com seu ponto de vista, são chamados de caminhos desorientadores. Observe que nem todo caminho de Aderbal é desorientador: se ele der duas voltas antes de entrar no relógio novamente não ficará com a impressão de que o sentido dos ponteiros do relógio mudou! |
|
CapVIII-pg4 |
|