|
|
CapVII-pg2 |
|
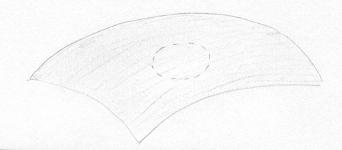
Suponha agora que temos uma superfície qualquer com característica de Euler X e removemos uma tampa, transformando-a numa nova superfície com característica de Euler X'. Qual é a relação entre X' e X? |
Primeiro localizamos onde será removida a tampa. |

|
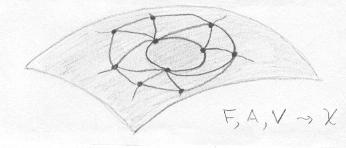
Escolhemos então uma triangulação da superfície em que a tampa a ser removida seja um dos triângulos. |
|
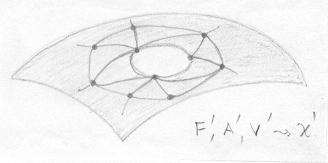
Quando tiramos a tampa, temos automaticamente uma triangulação para a nova superfície. |
|
A única diferença entre as duas é uma face. Isto é, F'=F-1, A'=A, V'=V. Logo X'= F'-A'+V'=(F-1)-A+V = X-1. |
Conclusão: remover uma tampa reduz em uma unidade a característica de Euler. Por exemplo, a esfera tem X=2. Tirando uma tampa, ficamos com o disco, que tem X=1. Tirando mais uma tampa, ficamos com o cilindro, que tem X=0. |
Outro exemplo é a superfície amarela da Página 1 do Capítulo III, que é um Toro menos três tampas. Como a característica de Euler do Toro é igual a zero, essa superfície tem característica de Euler igual a -3. |
|
CapVII-pg2 |
|