|
|
CapVII-pg1 |
|
Cortes e colagens nos serviram até agora para, junto com as deformações (isotopias), alterar a maneira como uma superfície se localiza no espaço sem mudar essencialmente suas propriedades básicas: conectividade simples, propriedade de Jordan, número de componentes de bordo e a característica de Euler. |
Os cortes e colagens também nos servirão para construir novas superfícies a partir de outras já existentes. Vamos discutir agora duas dessas operações e como a característica de Euler é afetada por elas. |
Remoção e adição de tampas. |
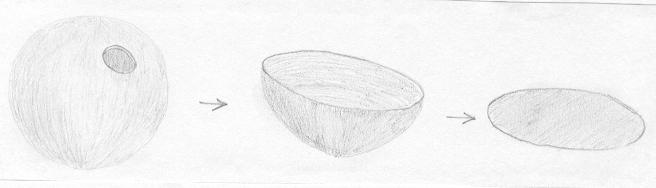
Em uma superfície qualquer, podemos remover uma "tampa", isto é, uma região que é isotópica a um disco. Veja dois exemplos. |
Às vezes também podemos fazer a operação inversa, que é a de adicionar uma tampa. Isso não é possível em superfícies sem bordo, como a Esfera, o Toro ou o Bitoro. Mesmo havendo bordo, pode não ser possível adicionar a tampa sem provocar uma auto-interseção na superfície resultante. |
O cilindro, por exemplo, pode ser completado com duas tampas. A nova superfície será isotópica à esfera. |
Por outro lado, o cilindro pode ser obtido da esfera pela remoção de duas tampas. Se removêssemos apenas uma tampa da esfera, obteríamos uma superfície isotópica ao disco. |

|
|
CapVII-pg1 |
|