|
|
CapVI-pg5 |
|
Na verdade, tudo o que dissemos para a esfera com X=2 vale para o toro com X=0. Temos só que ter cuidado com as propriedades estabelecidas para os grafos! (Muitas vezes, para simplificar as coisas, os matemáticos preferem usar como grafos as triangulações.) |
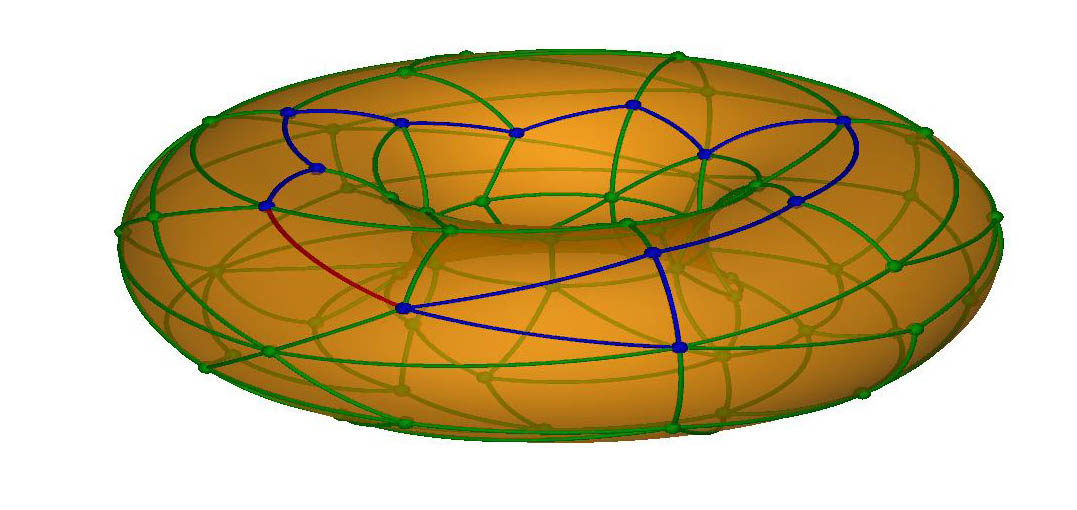
A demonstração do Teorema de Euler não funciona para o Toro porque ele não é uma superfície de Jordan. Lembre que usamos essa propriedade, válida na Esfera, quando uma nova aresta ligava dois vértices já pintados, o que causava uma separação em duas regiões. Observe na figura abaixo como a nova aresta (pintada em vermelho) não necessariamente separa o Toro em duas regiões! |

|
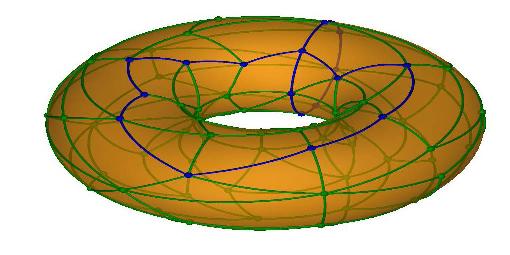
A maneira de contornar esse problema é começar com o conjunto de arestas e vértices pintados da seguinte forma. |
|
O leitor pode perceber que o número de regiões (denotado novamente por FP) separadas pelas arestas pintadas é 1, e além disso há uma aresta a mais do que o número de vértices, isto é, AP = VP+1. Então XP tem que ser zero, nesse estágio. Além disso, a partir desta situação, sempre que uma nova aresta ligar dois vértices já pintados haverá a separação em duas regiões, e o argumento usado na demonstração do Teorema de Euler continuará válido. Isso mostra que X tem que ser zero para superfícies isotópicas ao Toro. |
Não demonstraremos a seguinte afirmação, mas não é difícil de acreditar nela pelo que já vimos nos casos da Esfera e do Toro. Toda superfície (com ou sem bordo) tem essa mesma propriedade: "existe um número X tal que para toda triangulação (ou grafo conexo com faces poligonais) da superfície, o número de faces (F) menos o número de arestas (A) mais o número de vértices (V) é sempre igual a X". |
Esse número é chamado de Característica de Euler da superfície. Como vimos, a Característica de Euler da Esfera é igual a 2 e a do Toro é igual a zero. |
Calculemos a característica de Euler do Disco e do Anel. Observemos que essas superfícies têm bordo, e nesse caso temos que adaptar a triangulação ao bordo. |
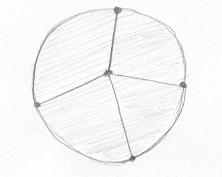
Disco. Escolhemos uma triangulação qualquer do disco. |
|
Experimente outra triangulação e você terá o mesmo resultado: X = 1. |
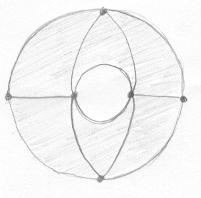
Anel. A característica de Euler do Anel é zero, como mostra a ilustração abaixo. |
|
É importante notar que a Característica de Euler não se altera sob isotopias, pois os números de faces, arestas e vértices se mantêm. Não é difícil de ver que também os homeomorfismos preservam a Característica de Euler. Nesse caso, sabendo previamente onde será cortada a superfície, convém adaptar a triangulação de modo que o corte seja feito sobre as arestas. Assim, ao se colar novamente, os números de faces, arestas e vértices são preservados. |
Por exemplo, como o Cilindro é isotópico ao Anel, e o Anel tem Característica de Euler igual a zero, então o Cilindro também tem Característica de Euler igual a zero. Qualquer superfície homeomorfa ao Cilindro também tem a mesma característica de Euler. |
|
CapVI-pg5 |
|