
|
|
CapVI-pg4 |
|
Muito bem, será que o Teorema de Euler é realmente verdadeiro? O leitor ainda desconfiado poderia examinar o poliedro mostrado abaixo. Observe que há 9 faces (todas poligonais), 18 arestas e 9 vértices, e portanto X = F-A+V = 0! |

|
Isso significa que o Teorema de Euler não se aplica para essa figura! De fato, não há nenhum problema nisso: o Teorema de Euler foi demonstrado para superfícies que são isotópicas à Esfera, o que não é o caso desse poliedro! |
Na verdade, o poliedro mostrado é isotópico ao Toro. Veja abaixo. |
Será que podemos associar ao Toro o número X=0, assim como associamos o número X=2 à Esfera? |
Antes de responder a essa pergunta, vejamos o seguinte exemplo, que também é um poliedro isotópico ao Toro. |
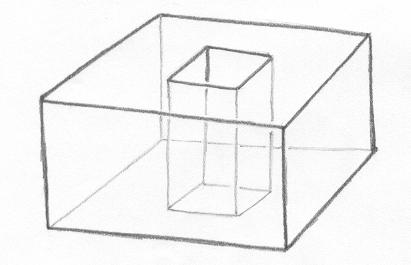
|
Ôpa! Não deu zero!! Aparentemente não é garantido que X seja o mesmo em duas figuras isotópicas ao Toro! |
Na verdade o erro é nosso. Não fomos rigorosos e acabamos por permitir duas faces (a de cima e a de baixo) isotópicas a um Anel, e portanto não poligonais! |
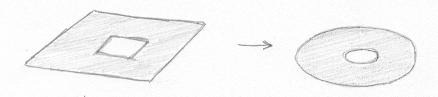
|
Se acrescentarmos duas arestas em cada uma, como na figura abaixo, então obteremos X = 0. |
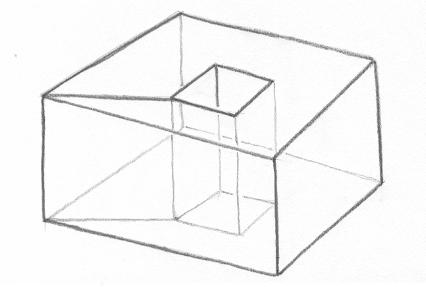
|
|
CapVI-pg4 |
|