
|
|
CapVI-pg3 |
|
Mostraremos agora que vale a seguinte afirma��o: "dado qualquer grafo sobre a esfera, conexo e com faces poligonais, se contarmos o n�mero de faces F, o n�mero de arestas A e o n�mero de v�rtices V, ent�o o n�mero X = F - A + V ser� igual a 2". |
Podemos pensar do seguinte jeito. Queremos calcular X para um determinado grafo, por exemplo o mesmo que j� mostramos antes. |

|
Faremos um racioc�nio por etapas. Para contar arestas e v�rtices, usaremos outra cor, e come�aremos com os v�rtices e arestas que delimitam uma das faces j� pintados, como mostra a figura abaixo. |

|
Contaremos os v�rtices pintados (VP), as arestas pintadas (AP), e o n�mero de regi�es separadas pelas arestas pintadas (FP). Na situa��o inicial mostrada acima, FP = 2, e AP = VP, isto �, o n�mero de v�rtices pintados � igual ao n�mero de arestas pintadas. Ent�o XP = FP -AP + VP tem que ser igual a 2!. |
O racioc�nio continua da seguinte forma. Em cada etapa pintaremos uma aresta, com as seguintes regras:
|
|
Para ilustrar melhor, usaremos a cor vermelha para indicar os novos elementos pintados de uma etapa para outra. As duas situa��es mostradas abaixo s�o as �nicas poss�veis: ou a nova aresta liga um v�rtice j� pintado a um outro n�o pintado, ou ela liga dois v�rtices j� pintados. |
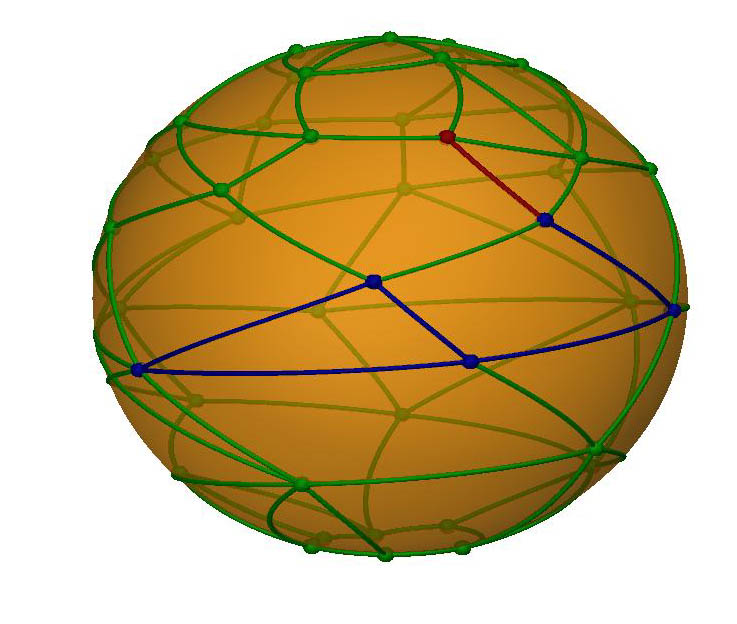
|
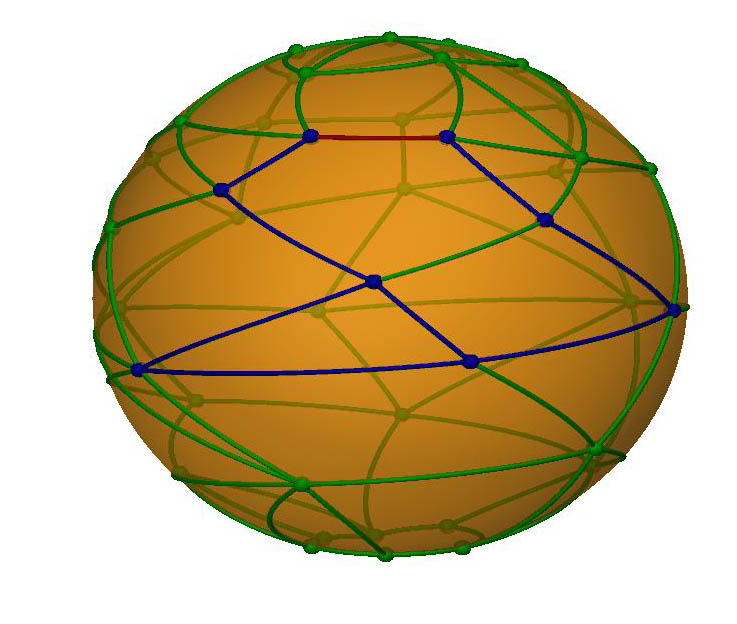
|
No caso em que um novo v�rtice � ligado nenhuma nova regi�o separada pelas arestas azuis � criada, ent�o o n�mero FP se mant�m. Por outro lado, uma aresta e um v�rtice s�o acrescentados, o que faz com que AP passe para AP+1 e VP passe para VP+1. Ent�o XP passa para FP - (AP+1) + (VP+1), e isso � igual ao pr�prio XP! Conclu�mos que neste caso o n�mero XP se mant�m inalterado! |
No outro caso a nova aresta liga dois v�rtices j� pintados. Como eles j� estavam pintados, ent�o j� existia uma seq��ncia de arestas os ligando, e ao acrescentarmos a nova aresta, uma curva fechada � formada. Como a Esfera � uma superf�cie de Jordan, o n�mero de regi�es separados pela aresta pintada passa de FP para FP+1. Por outro lado, nenhum novo v�rtice foi pintado (VP se mant�m) e uma aresta foi acrescentada (AP passa para AP+1. Ent�o XP passa para (FP+1)-(AP+1)+VP, ou seja, tamb�m n�o muda! |
Conclus�o: em nenhum dos casos a passagem de uma etapa para outra altera o n�mero XP. Como na configura��o inicial ele era igual a 2, assim ele ir� se manter at� o final, quando todos as arestas e v�rtices estiverem pintados. Mas quando isso acontecer, FP ser� igual a F, AP igual a A, VP igual a V e, � claro, XP igual a X. Logo, X = 2!!! |
Isso demonstra o Teorema de Euler! |
|
CapVI-pg3 |
|