Aos efeitos de uma melhor conceituação do projeto, dividimos o mesmo em cinco linhas principais. Vale a pena salientar, no entanto, que existe um alto número de interações entre estas linhas. Elas são: programação linear e complementaridade linear, problemas estruturados, otimização diferenciável, otimização não diferenciável e otimização em espaços de dimensão infinita.
1. Programação linear e complementaridade linear
As áreas de programação linear e complementaridade linear tiveram um grande desenvolvimento nos últimos doze anos, a partir da publicação do algoritmo de Karmarkar. Participamos desse processo desde o princípio, e temos uma boa experiência acumulada, várias publicações e reconhecimento internacional.
Existem atualmente muitos algoritmos eficientes para esses problemas, tanto do ponto de vista teórico (métodos com terminação polinomial e métodos com taxas de convergência quadrática), como do ponto de vista prático (pacotes computacionais que resolvem grandes problemas). A área continua no entanto muito viva, com grandes questões em aberto. Nossa pesquisa pretende avançar sobre algumas dessas questões, descritas a seguir.
Os algoritmos mais importantes evoluem em pontos pertencentes a uma vizinhança
da curva conhecida como ``trajetória central'' do problema. Estudamos a
eficiência do algoritmo de Newton para aproximar-se da trajetória a partir de
pontos bastante afastados dela (pontos em vizinhanças definidas pela norma
![]() ). Pretendemos caracterizar o comportamento assintótico do
método de Newton à medida que os pontos aproximam-se da face ótima, tentando
obter uma explicação parcial da razão por que os algoritmos mostram resultados
práticos muito superiores aos previstos pelos estudos teóricos de pior caso.
). Pretendemos caracterizar o comportamento assintótico do
método de Newton à medida que os pontos aproximam-se da face ótima, tentando
obter uma explicação parcial da razão por que os algoritmos mostram resultados
práticos muito superiores aos previstos pelos estudos teóricos de pior caso.
A terminação dos algoritmos tem sido objeto de pesquisas recentes, resultando em
algoritmos cuja complexidade depende de novos números de condicionamento
associados aos dados dos problemas (em vez do pouco satisfatório comprimento
da entrada de dados). Estamos trabalhando sobre os resultados de Vavasis e Ye,
tentando melhorar seu algoritmo. Estudamos também a complexidade de algoritmos
de pontos interiores não viáveis, tentando resolver o seguinte problema
aberto: a melhor complexidade que se obtem para esses algoritmos é de
O(nL) passos de Newton, o que parece indicar que não se está seguindo as
trajetórias mais eficientes. Nossa meta é baixar a complexidade desses
algoritmos para 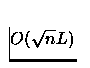 passos.
passos.
A partir de um bom entendimento do comportamento de algoritmos de pontos interiores não viáveis, nossa meta a médio prazo é trabalhar sobre sua extensão a problemas de programação não linear diferenciável com restrições de desigualdade. Estudamos também algoritmos de penalidades baseadas em suavizações da função penalidade exata. Nesses algoritmos utilizamos dois parâmetros, um responsável pelo grau de suavização, e o outro responsável pela inclinação da penalidade. Temos já resultados mostrando que (sob condições bastante razoáveis) quando a região viável tem interior não vazio, após um número finito de iterações o algoritmo torna-se definitivamente um método de pontos interiores. Pretendemos estudar as propriedades desses métodos.
É também parte do projeto o estudo e desenvolvimento de outros métodos para programação linear, que, embora sendo também de ponto interior, não fazem parte da linhagem resenhada acima.
Em primeiro lugar, mencionamos os métodos derivados da noção de trajetória central para desigualdades variacionais com barreiras genéricas, desenvolvidos recentemente por Iusem, Svaiter e da Cruz. Considera-se o problema de programação linear como um caso particular dos problemas de desigualdades variacionais, discutidos no item 4 desta seção. Utilizando a barreira logarítmica para as variáveis primais e um termo de regulariza cão quadrático para as variáveis duais, irrestritas em sinal, gera-se uma trajetória central semelhante à discutida anteriormente, porém com várias propriedades específicas. Modificando adequadamente os métodos "path-following" usados no caso da trajetória central decorrente da barreira puramente logarítmica, é possível formular um algoritmo primal relacionado com o método de trajetória central de Gonzaga, e um algoritmo primal-dual não viável relacionado com o método de Kojima, Megiddo e Nizumo. Já foi demonstrada a convergência finita destes métodos.
O objetivo do projeto no que diz a estes métodos consiste no estudo de diversas variantes dos dois algoritmos básicos já formulados, assim como no estudo da sua possível convergência polinomial, para escolhas particulares dos parâmetros e funções auxiliares utilizadas, que em certos casos são autoconcordantes no sentido de Nesterov e Nemirovski.
Finalmente consideramos o estudo de métodos para programação linear do tipo ``ação de linha". Estes métodos, em geral, não geram algoritmos polinomiais. No entanto, as suas fórmulas iterativas são extremamente simples, não modificam a matriz de dados através do processo iterativo e não requerem solução de sistemas lineares em cada iteração. São portanto úteis no caso de problemas de programação linear com matrizes muito grandes e esparsas, como as que aparecem, por exemplo, em problemas de tomografia computadorizada. Mencionamos em particular dois métodos de este tipo. O primeiro é o algoritmo para otimização convexa desenvolvido por Iusem e Zenios. Este método tem se mostrado computacionalmente eficiente, quando implementado em computadores com um grande número de processadores paralelos, na resolução de problemas de fluxos de rede generalizados, apresentada em vários trabalhos de Zenios, Nielsen e colaboradores. O segundo é o algoritmo para pontos de sela utilizando funções de Bregman, recentemente desenvolvido por Iusem e Kallio. O método, relacionado com o algoritmo para pontos de sela de Kallio-Ruszczynski e com o método de Korpolevich para desigualdades variacionais, já foi também testado computacionalmente, com resultados parciais alentadores.
O objetivo do projeto no referente a estes métodos consiste no seu aprimoramento e extensão. Particularmente, estudaremos melhores técnicas de pré-escalamento (``scaling") da matriz do problema, que tem se mostrado crucial nas experiências numéricas realizadas até agora.
2. Problemas estruturados
Quanto as técnicas específicas para problemas estruturados, que têm sido especialmente estudadas pelos pesquisadores do IME-USP, o objetivo principal é o aproveitamento em algoritmos de otimização de tal estrutura. Podem-se considerar duas linhas básicas:
1- Aproveitamento em termos de decomposição e políticas distribuidas.
2- Aproveitamento em termos computacionais.
Os problemas estruturados de fundamental interesse para o projeto são:
1- Redes de computadores e sistemas de manufatura em decomposição e políticas descentralizadas.
2- Planejamento multiperíodo em problemas de produção, economia ou finanças.
Na parte de decomposição e descentralização, buscamos obter novos métodos de projeto de redes e contribuições à incipiente teoria dos sistemas compartilhados com disputa por recursos. Problemas típicos ora em estudo são: problemas de projeto de redes de computadores com restrição de equanimidade, caracterização dos vértices de ``multi-commodity flow" para CFA (``capacity and flow assignment") global, ``bounds" para redes de filas e políticas estabilizadoras para em controle descentralizado de sistemas de manufatura.
Na parte de métodos computacionais busca-se unir a pesquisa na área de métodos numéricos (em particular para programação estocástica) com a geração de códigos que possam ser utilizados no mínimo como protótipos de ``solvers" em classes de problemas reais. Em termos de pesquisa e desenvolvimento os tópicos onde nossa atividade está centrada são: métodos para planejamento multiperíodo e determinação e visualisação de superfícies ótimas para problemas de administração de portfólio.
A longo prazo, esta linha tem o ambicioso objetivo de contribuir para os fundamentos de uma Teoria de Sistemas para sistemas distribuidos com disputa de recursos.
Todos estes objetivos são ancorados na frase acima, que apesar de aparentemente altissonante tem relevância prática e teórica como pode ser melhor visto pelos equívocos que ainda hoje se perpetram e pelo nível simples de questões ainda abertas. Por exemplo, ainda é comum referências importantes na área de otimização e redes de computação indicarem erroneamente que a complexidade dos projetos de redes deve-se fortemente à minimalidade local do problema de designação de capacidades, quando sob hipóteses usuais provamos que este problema só tem mínimo global. Em relação aos sistemas de filas estocásticos o simples caso de uma rede fechada de dois servidores com quatro "buffers" , com simetria, só teve seu comportamento limite resolvido em junho de 1996. Em relação à otimização de sistemas tipo manufatura ainda se publica uma imensa quantidade de artigos na abordagem dita de controle hierárquico, sendo que o grupo de pesquisadores do IME-USP provou que para custos médios separáveis (do tipo correspondente a quase metade da literatura), o controle ótimo considerando indivisibilidades e tempos de ``set-up" é, em geral, completamente desvinculado da trajetória do problema relaxado, dita trajetória de alto nível. Assim sendo, a pesquisa nesta área tem uma relevância teórica e atualidade claras, em particular se lembrarmos que alguns dos resultados teóricos transplantados para a prática estão entre aqueles cuja incorreção é citada acima.
Colabora nesta área o Dr. O. Porto da PUC-RJ.
No contexto internacional, a AMS e a SIAM ao definirem seu ``Joint Summer Workshop", indicaram implicitamente a área de sistemas distribuidos estocásticos como de alta relevância no contexto teórico. Ao mesmo tempo, as diretrizes da NSF indicam tal área como fundamental em termos aplicados pelo seu impacto na competitividade para comércio internacional. No contexto nacional, a questão de competitividade adquire uma dimensão cada vez maior com a realidade da abertura comercial do país.
Quanto ao aproveitamento computacional, nosso objetivo é o desenvolvimento de ``solvers" de programação matemática especialmente adaptados para otimização de problemas com estrutura (forma) angular blocada por linhas (RBAF - Row Block Angular Form), e forma angular blocada por linhas aninhada (NRBAF - Nested Row Block Angular Form). Esta linha de pesquisa da prosseguimento a vários resultados já obtidos na área pelos pesquisadores do grupo.
Esperamos que estes ``solvers" possam competir com ``solvers" comerciais como por exemplo, os ``solvers" da Optimization Subroutine Library da IBM (OSL-IBM). Isto explica o interesse de empresas comerciais como a UniSoma de Campinas. Os softwares MultiFor e DyFor da empresa UniSoma para aplicação agro-industrial resolvem problemas de otimização de múltiplas misturas, com estrutura RBAF, e problemas de otimização multi-período, com estrutura NRBAF.
Na geração destes ``solvers", duas características do problema são cruciais para atingir o alto desempenho desejado: esparsidade e estrutura.
Quanto à esparsidade,
grande parte do processamento de dados em ciência envolve
computação numérica, e a maior parte desta
computação numérica são rotinas básicas de
álgebra linear. Várias aplicações em engenharia,
física, pesquisa operacional, administração ou
matemática, geram problemas lineares cujas matrizes são esparsas
(entre tantos outros: resolução de equações
diferenciais, análise de sistemas, circuitos ou estruturas,
programação linear e não linear, otimização de
fluxos em redes, etc...). Ademais, observa-se que a densidade destas
matrizes decresce com a dimensão do problema: tipicamente apenas da
ordem 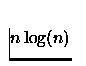 dos n2 elementos na matriz são não nulos.
Assim, quanto maiores e mais complexos os problemas (e usuários
sempre querem resolver modelos maiores), mais importante se torna usar
eficientemente a esparsidade e a estrutura das matrizes envolvidas.
Por exemplo, na área de otimização, problemas de
aplicação industrial hoje considerados de médio porte
envolvem milhares de equações, sendo a maioria destes problemas
altamente estruturados, muito esparsos, e usando mais de 99% do tempo de
resolução em rotinas básicas de álgebra linear!
dos n2 elementos na matriz são não nulos.
Assim, quanto maiores e mais complexos os problemas (e usuários
sempre querem resolver modelos maiores), mais importante se torna usar
eficientemente a esparsidade e a estrutura das matrizes envolvidas.
Por exemplo, na área de otimização, problemas de
aplicação industrial hoje considerados de médio porte
envolvem milhares de equações, sendo a maioria destes problemas
altamente estruturados, muito esparsos, e usando mais de 99% do tempo de
resolução em rotinas básicas de álgebra linear!
No que diz à estrutura, o problema básico é como resolver eficientemente sistemas esparsos cujos elementos não nulos estão dispostos com uma certa regularidade na matriz de coeficientes.
``Solvers" comerciais, como por exemplo o OSL (Optimization Suboutine Library da IBM), utilizam eficientemente a esparsidade geral dos problemas de médio e grande porte. Todavia, a estrutura de um problema só pode ser bem aproveitada por um ``solver" especialmente desenvolvido para uma classe de problemas com aquela estrutura. Ademais, o ``solver" terá de saber a priori, ou então reconhecer automaticamente, detalhes desta estrutura (e.g. dimensão dos blocos e sub-blocos) antes de iniciar a fase de resolução numérica do problema.
Existem na literatura duas abordagens clássicas para resolução de problemas de otimização estruturados (especialmente para estrutura bloco angular): os métodos de decomposição e os métodos estruturais, cada qual apresentando vantagens distintas:
Os métodos de decomposição mapeiam o problema original em vários sub-problemas acoplados. A estrutura do problema original é refletida na estrutura do acoplamento. No caso dos problemas bloco angulares, temos um sub-problema principal, ou "mestre" que devemos otimizar em função da solução dos demais sub-problemas, os problemas "auxiliares". Uma série de soluções iterativas mestre-auxiliares converge para a solução do problema original. Exemplos desta abordagem são os métodos de Dantzig-Wolf e Rosen. Este último foi utilizado no sistema MultiFor para resolver problemas bem menores que os resolvidos no sistema DyFor pelo ``solver" OSL.
Os métodos estruturais resolvem diretamente o problema original. A estrutura do problema é aproveitada num nível mais baixo, preservando a estrutura e a esparsidade da "fatoração da base" no algoritmo de restrições ativas.
Comparativamente, os métodos de decomposição são bastante fáceis de implementar (em comparação ao esforço de desenvolvimento), sendo basicamente um ``batch" ou ``loop exterior" invocando um ``solver" para os sub-problemas. Os métodos estruturais são extremamente eficientes, porém de implementação muito trabalhosa, dependendo inclusive de sub-rotinas especiais de álgebra linear computacional. Métodos estruturais são especialmente adequados para problemas de análise paramétrica e re-otimização (``partida quente") que corresponde á situação de uso típica de algumas aplicações deste projeto.
3. Otimização diferenciável
Os algoritmos práticos existentes no mercado para minimização de funções com restrições, que contam com software desenvolvido e disponível pelo menos para a comunidade científica, correspondem a três grandes protótipos:
(a) Algoritmos ``factíveis", do tipo GRG, ``restoration algorithms" e derivados.
(b) Algoritmos de penalização e ``Lagrangeano aumentado"
(c) Algoritmos de Programação Quadrática Sequencial (SQP).
Os pesquisadores do IMECC-UNICAMP participantes do núcleo já realizaram um incipiente trabalho no desenvolvimento de métodos de tipo (c) para problemas de grande porte, nos quais o problema da infactibilidade do sub-problema quadrático foi resolvido com recursos teoricamente consistentes. Tenciona-se aprofundar essas técnicas e, ao mesmo tempo, conectá-las com uma família de algoritmos ``semi-factíveis'', no sentido em que o progresso em cada iteração rumo a factibilidade se sustenta na própria função de restrições e não no seu modelo linear (como em SQP).
Os algoritmos de Lagrangeano aumentado descansam em implementações eficientes de métodos para minimização em caixas n-dimensionais, sobretudo em algoritmos para problemas de grande porte desse tipo. Na UNICAMP possui-se um software desenvolvido e razoavelmente consolidado para esses problemas (chamado BOX-QUACAN). Melhoramentos desse software serão tentados através da introdução de precondicionadores dos sub-algoritmos do tipo gradiente-conjugado inseridos para minimização nas faces das caixas e mediante uma técnica denominada de ``hot-starts'' para produzir, como seu nome indica, aproximações iniciais suficientemente boas na resolução dos sub-problemas newtonianos.
Existem também incipientes desenvolvimentos no sentido de afastar o problema da instabilidade na penalização externa clássica (e, em consequência, no Lagrangeano aumentado). A idéia subjaz nos algoritmos de Programação Quadrática Recursiva (RQP) (não confundir com SQP) de Bartholomew-Biggs e outros autores, e está sendo explorada pelos pesquisadores do IMECC-UNICAMP, visando inclusive melhores implementações de RQP.
No que diz à área de sistemas de equações, está sendo finalizado um ``survey'' sobre a área, destinado a aparecer no Handbook of Numerical Analysis dirigido por P. L. Lions, em colaboração com o grupo de J.E. Dennis de Rice University. A extensão de algoritmos para problemas não-diferenciáveis, o aproveitamento de estruturas especiais e a globalização (convergência independente do ponto inicial) são os principais aspectos considerados no momento.
Dentro da vasta literatura recente sobre complementaridade, inequações variacionais e problemas relacionados, a linha a ser desenvolvida no projeto tem a seguinte estrutura: para cada problema define-se um problema de otimização (geralmente com restrições simples) que equivale ao problema original do ponto de vista dos seus mínimos globais e tal que, em determinadas condições, os pontos estacionários são também soluções do problema original. Dessa maneira, o VIP (``variational inequality problem") e problemas análogos podem ser resolvidos usando técnicas bem consolidadas de minimização com restrições simples.
Mencionamos a seguir a utilização destas técnicas em vários problemas aplicados.
Através de colaboração com o Instituto de Física da UNICAMP está sendo desenvolvido um método de ``pointwise constrained minimization'' para a computação de parâmetros óticos de filmes finos. O algoritmo básico já foi apresentado em congressos de física no exterior e parece representar um avanço significativo do ponto de vista da física aplicada.
Por outro lado, a tecnologia de Lagrangeano aumentado associada ao software BOX-QUACAN vem sendo aplicada com sucesso preliminar a problemas de mecânica. Nesta linha, trabalha-se em colaboração com o grupo do Prof. Z. Dostal, da Universidade de Ostrava.
É também parte do projeto o aprimoramento dos métodos de regiões e confiança para otimização irrestrita. As técnicas usadas atualmente implementam os métodos quasi-Newton tipo secante (Broyden, BFGS, etc.) através do procedimento chamado ``double dog leg". O objetivo nesta área se baseia na minimização exata do modelo quadrático na interseção da região de confiança com a variedade afim de dimensão dois que contém o iterado corrente e é paralela ao subespaço gerado pelo gradiente aproximado e a direção de Newton aproximada. A região de confiança é escolhida via um critério tipo Armijo. Este método encontra-se atualmente em fase de estudos iniciais. Pretende-se comparar numericamente o novo método com as técnicas ``double dog leg".
Finalmente, consideramos o estudo de métodos para programação positiva semi-definida. O problema consiste em achar a matriz que minimiza a distância a uma matriz dada, medida pela norma de Frobenius. A matriz deve satisfazer certas restrições lineares e ser simétrica e positiva semi-definida. Atualmente, o método mais eficiente para este problema é o de Dijkstra-Han, que pertence à família de métodos de ação de linha. Nas implementações atuais, somente problemas de pequeno porte são tratáveis. O objetivo do projeto nesta área consiste em aplicar a este problema métodos de ação de linha desenvolvidos por B.F. Svaiter na sua tese de doutorado, a partir da sua nova teoria para dualidade em programação convexa, visando resolver eficientemente problemas de porte maior que o comportado pelo algoritmo de Dijkstra-Han.
Dentro das potenciais aplicações destes, uma área na qual esperamos um impacto significativo é a de problemas inversos. Mais especificamente, temos as seguintes aplicações em mente: tomografia na presença de difusão, prospecção de petróleo, e estratégias em mercados de opções. Nestas areas, o grupo do IMPA conta com a participação de J. P. Zubelli, que conjuntamente com A. Grünbaum, de U. C. Berkeley, desenvolveu um método para a reconstrução do interior de objetos na presença de espalhamento e difusão da radiação. Esta versão não linear de tomografia apresenta-se como uma alternativa para situações nas quais é interessante usar-se radiações de baixa energia, um exemplo sendo o caso de radiação infra-vermelha. Devido ao aumento da complexidade do problema pela não linearidade tornam-se necessário algoritmos altamente eficientes para a viabilização dos métodos.
4. Otimização não diferenciável
Os problemas de otimização não diferenciável tem sido intensamente estudados durante os últimos anos pelos pesquisadores do grupo de otimização do IMPA. O ponto de partida tem sido o ``método de ponto proximal", originado no estudo de problemas mal postos na escola de Tikhonov nos anos cinqüenta, e formulado como método de otimização por Rockafellar nos anos 70. O método não é a princípio um algoritmo diretamente implementável, mas um procedimento conceitual, que converte o problema original numa seqüência de problemas melhor comportados (e.g. com solução única). O método torna-se computacionalmente atraente quando os sub-problemas são também estruturalmente mais simples que o problema original. Um caso é a aplicação do método ao dual de um problema de programação convexa com restrições. Neste caso o método de ponto proximal recupera os métodos de Lagrangeano aumentado, que consiste em resolver uma seqüência de problemas irrestritos. Mas o método aplicado diretamente ao problema de programação convexa produz em geral problemas com as mesmas restrições que o problema original. Esta deficiência é corrigida nos métodos desenvolvidos no IMPA. Estes métodos substituem a distância quadrática por uma distância generalizada, chamada de Bregman, que atua como uma função de penalização interna, gerando métodos de ponto interior com sub-problemas irrestritos, e tem sido recentemente estendidos a problemas de desigualdades variacionais por Iusem, Burachik e outros autores.
Atualmente, o objetivo do projeto é o de recuperar para este tipo de algoritmos as
propriedades do método clássico de Rockafellar. Uma delas é que o algoritmo ainda converge
quando os sub-problemas são resolvidos somente em forma aproximada, sob a condição de
que os erros cometidos em cada iteração sejam somáveis. Os métodos de ponto proximal
com distâncias de Bregman não possuem esta propriedade em forma direta. Recentemente
Kiwiel mostrou que a propriedade é válida para problemas de otimização, se mudarmos
a noção de solução aproximada. Ele introduz uma noção adequada baseada no
conceito de ![]() -subgradiente de uma função convexa. Com o intuito de estender
o resultado às desigualdades variacionais, Burachik, Iusem e Svaiter desenvolveram recentemente
a noção de
-subgradiente de uma função convexa. Com o intuito de estender
o resultado às desigualdades variacionais, Burachik, Iusem e Svaiter desenvolveram recentemente
a noção de ![]() , para um operador monótono T, que guarda com T uma
relação semelhante à existente entre o
, para um operador monótono T, que guarda com T uma
relação semelhante à existente entre o ![]() -subdiferencial e o subdiferencial
de uma função convexa. Num trabalho recente, foram estabelecidas as principais propriedades
do novo objeto, incluindo a sua continuidade interior e exterior.
-subdiferencial e o subdiferencial
de uma função convexa. Num trabalho recente, foram estabelecidas as principais propriedades
do novo objeto, incluindo a sua continuidade interior e exterior.
Os objetivos do projeto em relação a esta questão são dois. No que diz
respeito aos métodos de ponto proximal
com funções de Bregman, estudarão-se especialmente métodos computacionais eficientes
para resolver os sub-problemas. A idéia é desenvolver métodos especialmente desenhados
para o término de regularização baseado em funções de Bregman. O segundo objetivo
consiste em utilizar a noção de ![]() para estender aos problemas de desigualdades
variacionais vários métodos relevantes para minimização de funções convexas não
diferenciáveis que utilizam o
para estender aos problemas de desigualdades
variacionais vários métodos relevantes para minimização de funções convexas não
diferenciáveis que utilizam o ![]() -subdiferencial, particularmente os métodos
de feixes (``bundle methods").
-subdiferencial, particularmente os métodos
de feixes (``bundle methods").
Outra questão a ser estudada no marco do projeto e a análise de convergência de algoritmos não monótonos. A maioria dos algoritmos usados tanto em otimização diferenciável quanto não diferenciável geram seqüências com certas propriedades de monotonia. Ou bem decresce a própria função objetivo, ou bem alguma outra medida de proximidade à solução (e.g. a distância ao conjunto de soluções). A análise torna-se consideravelmente mais difícil quando não há nenhuma ``função de Lyapunov" com comportamento monótono. Diversas técnicas têm sido propostas recentemente para abordar o problema de convergência de algoritmos não monótonos por Mangasarian, Bertsekas, Tseng, Solodov e outros.
O objetivo do projeto neste item consiste em avançar a respeito dos resultados já obtidos, tanto no que diz respeito a algoritmos intrinsicamente não monótonos, quanto no que diz respeito à perda de monotonicidade devido a perturbação nos dados e a solução inexata de sub-problemas. Isto é importante também para identificar algoritmos monótonos que são numericamente estáveis em situações de perturbação dos dados. Entre os métodos a serem estudados estão os métodos de direções viáveis de descida para otimização, algoritmos incrementais para treinamento de redes neurais e métodos de projeções para desigualdades variacionais.
5. Otimização em espaços de dimensão infinita
O projeta contempla o estudo de três problemas de otimização em dimensão infinita.
(i) Métodos de ponto proximal.
O método de ponto proximal foi apresentado por Rockafellar em espaços de Hilbert. Recentemente, Iusem e Burachik provaram que o método de ponto proximal com funções de Bregman é também convergente em espaços de Hilbert. O objetivo do projeto neste item consiste em estudar as propriedades tanto do método clássico como dos métodos com distâncias de Bregman em espaços de Banach.
(ii) Métodos para problemas de viabilidade convexa.
Os problemas de desigualdades variacionais podem ser vistos como um problema de
viabilidade convexa com infinitas restrições. Esta reformulação é
especialmente atraente no caso de espaços de dimensão infinita (especialmente
os espaços ![]() e Lp) onde os métodos convencionais para desigualdades
variacionais (e.g. o de Korpolevich, etc.) são de difícil aplicação. O objetivo
é achar um ponto que satisfaz ``quase todas" as restrições (no sentido da teoria
da medida). Recentemente, Butnariu, Censor e Reich apresentaram um método de este tipo
onde cada iterado é projetado em cada convexo, e o iterado seguinte é obtido integrando
estas projeções. Acontece que nos espaços mencionados acima a projeção
tomada com respeito a distância usual (baseada na norma do espaço) é de cálculo
difícil, mesmo quando os convexos são semi-espaços, como é o caso dos problemas
de desigualdades variacionais. No entanto, é mais fácil projetar com respeito a uma
função de Bregman apropriada (por exemplo, a gerada pela p-ésima potência da
norma, para os espaços
e Lp) onde os métodos convencionais para desigualdades
variacionais (e.g. o de Korpolevich, etc.) são de difícil aplicação. O objetivo
é achar um ponto que satisfaz ``quase todas" as restrições (no sentido da teoria
da medida). Recentemente, Butnariu, Censor e Reich apresentaram um método de este tipo
onde cada iterado é projetado em cada convexo, e o iterado seguinte é obtido integrando
estas projeções. Acontece que nos espaços mencionados acima a projeção
tomada com respeito a distância usual (baseada na norma do espaço) é de cálculo
difícil, mesmo quando os convexos são semi-espaços, como é o caso dos problemas
de desigualdades variacionais. No entanto, é mais fácil projetar com respeito a uma
função de Bregman apropriada (por exemplo, a gerada pela p-ésima potência da
norma, para os espaços ![]() e Lp). Este método, usando projeções de Bregman,
tem sido recentemente desenvolvido por Iusem e Butnariu. O objetivo do projeto quanto
a este item consiste em aprimorar o algoritmo recentemente formulado, e estender a sua
aplicação ao problema de achar pontos fixos de operadores monótonos em espaços
de Banach.
e Lp). Este método, usando projeções de Bregman,
tem sido recentemente desenvolvido por Iusem e Butnariu. O objetivo do projeto quanto
a este item consiste em aprimorar o algoritmo recentemente formulado, e estender a sua
aplicação ao problema de achar pontos fixos de operadores monótonos em espaços
de Banach.
(iii) Algoritmos tipo gradiente e gradiente projetado em espaços de Banach.
Os métodos de segunda ordem, com convergência quadrática ou ao menos superlinear, não
são apropriados em espaços de Banach, onde no entanto podem ser utilizados métodos
mais simples, como o do gradiente. No caso não diferenciável, as direções
dadas por subgradientes não são necessariamente de descida, tornando impossíveis
métodos com decrescimento dos valores funcionais. Nestes casos, o passo deve ser
determinado exogenamente. Recentemente, dois trabalhos de Alber, Iusem e Solodov provaram
a convergência quando os passos ![]() satisfazem
satisfazem 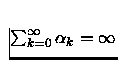 ,
,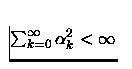 em espaços de Banach e Hilbert respectivamente.
O objetivo do projeto neste item consiste em estender este resultado ao caso em que
em espaços de Banach e Hilbert respectivamente.
O objetivo do projeto neste item consiste em estender este resultado ao caso em que
![]() satisfaz
satisfaz 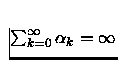 ,
, 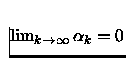 .
.
Além das atividades de pesquisa, o projeto do ncleo inclui ainda a realização de uma reunião internacional do mais alto nível, com a participação dos mais importantes pesquisadores nacionais e estrangeiros da área, em 1998.