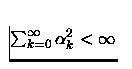 .
.Em Otimização resultados esperados, independentemente do assunto específico, sempre são variações do paradigma: ``eficiência prática (medida pela aplicação com êxito a problemas reais) e consistência teórica (representada por arcabouço teórico adequado)''.
Assim, para as diferentes áreas em desenvolvimento, almeja-se:
1. Programação linear e complementaridade linear
(i) Publicação de uma análise de complexidade de algoritmos preditores-corretores usando vizinhanças grandes da trajetória central.
(ii) Formulação e estudo da análise assintótica dos passos de Newton em algoritmos de trajetória central.
(iii) Se possível, obter a redução da complexidade de algoritmos de pontos interiores não viáveis, a partir do estudo de superfícies de centros inviáveis.
(iv) Estudo e tentativa de aprimoramento das técnicas de pontos interiores baseados em números de condicionamento dos dados.
(v) Publicação de análise do comportamento assintótico de algoritmos baseados em suavizações da barreira exata.
(vi) Elaboração e programação em MATLAB de um pacote de rotinas (toolbox) para o estudo de algoritmos de pontos interiores.
(vii) Formulação e implementação de versões mais eficientes dos algoritmos de Iusem-Kallio (estudando novas técnicas de pré-escalamento), e de Iusem-Zenios, assim como a obtenção de novos resultados de convergência para os métodos de programação linear baseados em trajetórias centrais para desigualdades variacionais com barreiras gerais.
2. Problemas estruturados
(i) Em relação aos projetos de redes, encontrar uma solução para o problema de projeto de rede considerando não somente a restrição de retardo médio, mas também restrições de máximo retardo em relação a dados pares origem destino (pelo menos para a questão de designação de capacidades).
(ii) Também em relação aos projetos de redes, verificar a plausibilidade da adaptação de resultados de minimização de funções côncavas em poliedros, para o problema de designação de fluxos e capacidades. Para tal não somente é necessário caracterizar os vértices do poliedro de fluxos físicos (associado ao ``multicommodity flow"), como é necessário saber caracterizar adjacências.
(iii) Em relação às redes de filas, expandir os resultados já obtidos de limitação funcional de desempenho de redes de filas com o uso de programação linear e investigar as limitações desta abordagem. Na medida que estes resultados de limitação funcional são os mais fortes conhecidos na área, a questão acima é altamente relevante.
(iv) Em relação aos sistemas distribuidos com escalonamento descentralizado, além de expandir os resultados na atual linha de pesquisa em sistemas de manufaturas descentralizados, pretende-se utilizar esta abordagem no problema de controle descentralizado de redes de computadores.
(v) Em relação aos problemas de planejamento multi-período pretende-se implementar um ``solver" que seja competitivo com ``solvers" comerciais, como GAMS-Minos. Este ``solver" estará baseado em resultados teóricos previamente obtidos de aproveitamento de estrutura por métodos em operações básicas de álgebra linear computacional.
(vi) Também em relação aos problemas de planejamento multi-período pretende-se explorar as possibilidades de paralelização dos algoritmos a serem desenvolvidos. Neste esforco antev-se a colaboração com o grupo de pesquisa do Prof. Siang, e a utilização do computador com processadores em paralelo PARSITEC recentemente doado ao IME-USP pela Comunidade Européia em função dos projetos deste grupo.
3. Otimização diferenciável
(i) Completar uma teoria global de convergência de métodos semi-factíveis para programação não-linear, paralelamente a uma boa implementação para problemas de grande porte.
(ii) Consolidar a teoria e implementação de algoritmos globalmente convergentes para certos sistemas não-diferenciáveis.
(iii) Produzir uma nova versão, com precondicionadores e ``hot-starts" eficientes, para BOX-QUACAN.
(iv) Avançar no sentido da compreensão e eliminação dos problemas de instabilidade associados à penalização externa.
(v) Desenvolver algoritmos específicos para desigualdades variacionais e problemas relacionados usando o paradigma da minimização com restrições simples.
(vi) Aprofundar a utilização das técnicas desenvolvidas para problemas práticos.
(vii) Implementar alternativas à técnica do ``double dog leg" nos métodos quase-Newton com regiões de confiança, e comparar numericamente as alternativas com esta técnica.
(viii) Implementar o novo método de ação de linha para programação positiva semi-definida, e utilizar este método em aplicações estatísticas.
4. Otimização não diferenciável
(i) Formular e analisar métodos adequados para a resolução dos sub-problemas do método de ponto proximal com distâncias de Bregman.
(ii) Formular e analisar métodos de feixe para desigualdades variacionais.
(iii) Estender os resultados de estabilidade para métodos não monótonos recentemente obtidos por Solodov aos métodos de descida por coordenadas e métodos de partição de matrizes.
5. Otimização em espaços de dimensão infinita
(i) Estender aos espaços de Banach os resultados existentes para o método de ponto proximal em espaços de Hilbert.
(ii) Aprimorar o método de Butnariu-Iusem para o problema de viabilidade convexa em espaços de Banach con infinitas restrições.
(iii) Determinar as propriedades de convergência dos métodos
do gradiente e gradiente projetado sem a hipótese de
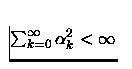 .
.
No que diz á relevância do projeto no seu conjunto, podem-se distinguir duas abordagens: em primeiro lugar a relevância acadêmica, ou seja a importância dos temas abordados no contexto da teoria da otimização. Não nos estenderemos particularmente neste ponto, sendo que todos os temas que constam do projeto são da maior importância atual na área e têm dado origem a uma vasta produção publicada nos melhores periódicos do tema. Uma pequena amostra pode ser encontrada nos ``curricula" dos pesquisadores integrantes do projeto, em anexo. Em segundo lugar, a relevância prática, ou seja a importância dos assuntos abordados nas aplicações. Sob este ponto de vista, destacamos que alguns dos temas desenvolvidos são de natureza mais teórica, com perspectivas de aplicação mais distantes, sendo que outros são de aplicação prática imediata. Mencionaremos somente dois exemplos destes últimos: os sistemas compartilhados com disputa de recursos e os métodos de planejamento multi-período.
A relevância da teoria dos sistemas compartilhados com disputa por recursos é clara e, em particular, a AMS-SIAM elegeu em 96 como área prioritária em matemática aplicada o tópico "The mathematics of stochastics manufacturing systems", sendo que o grupo da USP não só foi lá representado, como teve um membro convidado como um dos poucos conferencistas plenários.
A relevância dos métodos de planejamento multi-período nos campos de economia, finanças e agro-indústria, é auto explicativa. Em termos de aplicação indicamos o interesse, participação e até suporte parcial obtido da BMeF - Bolsa de Mercadorias e de Futuros de São Paulo, de alguns bancos, assim como o interesse de firmas como a UniSoma de Campinas, em relação aos protótipos a serem desenvolvidos (note-se que a UniSoma tem prémios internacionais de aplicação concedidos pela ORSA - Operations Research Society of America).