Hashing

Livro de Sedgewick e Wayne: sec.3.4, p.458.  Website do livro: resumo sec.3.4, slides.  Código fonte, documentação, e dados de teste de todos os programas do livro: veja algs4.cs.​princeton.edu/​code/.

Esta página trata da implementação de TSs (tabelas de símbolos) por meio de tabelas de dispersão e tabelas de hash.  A teoria é simples mas o sucesso das implementações depende de truques práticos. Pode-se dizer que essas implementações envolvem mais arte que ciência.

Hashing tem dois ingredientes fundamentais: uma função de hashing e um mecanismo de resolução de colisões.

Ideias preliminares

• Exemplo 1:  Imagine um pequeno país (bem menos que 100 mil cidadãos) onde os números de CPF têm apenas 5 dígitos decimais. Considere a tabela que leva CPFs em nomes:

  chave  valor associado
  01555  Ronaldo
  01567  Pelé
  ...    ...
  80114  Maradona
  80320  Dunga
  95222  Romário
  

  Como armazenar a tabela? Resposta: vetor de 100 mil posições.  Use a própria chave como índice do vetor!

  • O vetor é conhecido com tabela de hash e
  • terá muitas posições vagas (desperdício de espaço), mas
  • a busca (get) e a inseção (put) serão extremamente rápidas.
• Exemplo 2:  Imagine uma lista ligada cujas chaves são nomes de pessoas. Suponha que a lista está em ordem alfabética.

  chave                 valor associado
  Antonio Silva         8536152  
  Arthur Costa          7210629  
  Bruno Carvalho        8536339  
  ...                   ...      
  Vitor Sales           8535922  
  Wellington Lima       5992240  
  Yan Ferreira          8536023  
  

  Para acelerar as buscas, divida a lista em 26 pedaços: os nomes que começam com "A", os que começam com "B", etc.  Nesse caso,

  • o vetor de 26 posições é a tabela de hash e
  • cada posição do vetor aponta para o começo de uma das listas.

Exercícios 1

1. Qual a diferença entre o exemplo dos CPFs acima e a implementação BinarySearchST já discutida?
2. Qual a diferença entre o exemplo das listas ligadas de nomes e a implementação SequentialSearchST já discutida?

Funções de hashing

• Uma tabela de dispersão ou tabela de hash (hash table) é um vetor cada uma de cujas posições armazena zero, uma, ou mais chaves (e valores associados).  (O conceito é propositalmente vago.)
• Parâmetros importantes:
  • M :  número de posições na tabela de hash
  • N :  número de chaves da tabela de símbolos
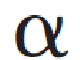  • = N/M :  fator de carga (load factor)
• Função de espalhamento ou função de hashing (hash function):  transforma cada chave em um índice da tabela de hash.
• A função de hashing responde a pergunta Em qual posição da tabela de hash devo colocar esta chave?.  A função de hashing espalha as chaves pela tabela de hash.
• A função de hashing associa um valor hash (hash value), entre 0 e M−1, a cada chave.
• No exemplo dos CPFs temos 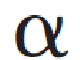 < 1  e a função de hashing é a identidade.
• No exemplo dos nomes de pessoas temos 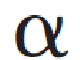 > 1  e a função de hashing é  nome.charAt(0).
• A função de hashing produz uma colisão quando duas chaves diferentes têm o mesmo valor hash e portanto são levadas à mesma posição da tabela de hash:

  

• Exemplo: Chaves são números de identificação (7 dígitos) de estudantes da universidade  e  M vale 100.

  8536152
  7210629
  8536339
  8536002
  ...
  8067490
  8536106
  8536169
  8531845
  

  Uma possível função de hashing:  2 primeiros dígitos da chave. Outra possibilidade: 2 dígitos do meio. Outra possibilidade: 2 últimos dígitos.  Qual dessas espalha melhor as chaves pelo intervalo 0 . . 99?

• Outro exemplo: função de hashing que leva qualquer número de CPF brasileiro (que tem nove dígitos) no correspondente dígito verificador (um número entre 0 e 99).  (Por exemplo, leva 111444777 em 35.)  O dígito verificador de um CPF depende de todos os dígitos do CPF.
• Ideal:  a função de hashing deveria usar todos os dígitos da chave; assim, chaves ligeiramente diferentes serão levadas em números muito diferentes.  (Subproduto: podemos usar o valor hash como checksum para verificar a integridade de um texto!)
• Escolha M e a função de hashing de modo a
  • diminuir o número de colisões;
  • espalhar bem as chaves pelo intervalo 0 . . M−1.

Função de hashing modular

• Que funções de hashing são usadas na prática?
• Se as chaves são inteiros positivos, podemos usar a função modular (resto da divisão por M):

  private int hash(int key) {
      return key % M;
  }
  

• Exemplos com M = 100 e com M = 97:

  

• Em hashing modular, é bom que M seja primo (por algum motivo não óbvio).
• No caso de strings, podemos iterar hashing modular sobre os caracteres da string:

  int h = 0;
  for (int i = 0; i < s.length(); i++)
      h = (31 * h + s.charAt(i)) % M;
  

  No lugar do multiplicador 31, poderia usar qualquer outro inteiro R, de preferência primo, mas suficientemente pequeno para que os cálculos não produzam overflow.

Exercícios 2

1. Qual o valor da expressão  key % M  se key é negativo?
2. Por que convém evitar overflow no cálculo do valor hash de uma string?
3. (SW 3.4.4)  Escreva um programa para encontrar valores de  a  e  M ,  com M o menor possível, tais que a função de hashing  (a * k) % M , que transforma a k-ésima letra do alfabeto em um valor hash, não produza colisões quando aplicada às chaves  S E A R C H X M P L .  (Isso é conhecido como função de hashing perfeita.)

Os métodos hashCode de Java

• Em Java, todo tipo-de-dados tem uma método padrão hashCode() que produz um inteiro entre −2³¹ e 2³¹−1 (aproximadamente 2 bilhões negativos a 2 bilhões positivos).  Exemplo:

  String s = StdIn.readString();
  int h = s.hashCode();
  

• Para converter o hashCode() em um número entre 0 e M−1, tome o resto da divisão por M.  Antes, é melhor desprezar o bit mais sigificativo para evitar que  %  lide com números negativos e produza um resultado negativo:

  private int hash(Key x) { 
      return (x.hashCode() & 0x7fffffff) % M; 
  }
  

  (O uso da máscara 0x7fffffff seria desnecessário se Java tivesse um tipo-de-dados unsigned int.)

O que se espera de uma função de hashing ideal

• Queremos uma função de hashing que
  • possa ser calculada eficientemente e
  • espalhe bem as chaves pelo intervalo 0 . . M−1.
• Exemplo: Valores hash calculados a partir do hashCode() padrão como acima para o conjunto de palavras (excluídas as repetidas) em tale.txt, com M = 97.  No histograma, cada barra dá o número de palavras que têm o valor hash indicado na ordenada. O histograma sugere que a função espalha bem as palavras.

  

• Hipótese do Hashing Uniforme:  Vamos supor que nossas funções de hashing distribuem as chaves pelo intervalo de inteiros 0 . . M−1 de maneira uniforme (todos os valores hash igualmente prováveis) e independente.
• Exemplo: Supõe-se que os números sorteados pela Loteria Federal são todos igualmente prováveis. Supõe-se também que são independentes:  só porque 888888888888 nunca foi sorteado, ele não tem maior probabilidade de sair no próximo sorteio.
• Na verdade, nenhuma função determinística satisfaz a Hipótese do Hashing Uniforme.  (Essa impossibilidade é uma questão profunda e fundamental em Ciência da Computação.)  Mas a hipótese é útil porque permite fazer cálculos para prever o desempenho aproximado de tabelas de hash.
• A função de hashing que usamos acima para analisar o livro tale.txt parece ser aproximadamente uniforme.

Exercícios 3

1. Elimine as palavras repetidas de tale.txt. Depois, faça um histograma como o mostrado acima mas usando M = 100.
2. Faça um histograma como o mostrado acima para as palavras de tale.txt (sem repetições), com M = 97, mas alguma função de hashing diferente da usada acima.
3. Faça um histograma como o acima para as palavras de quincasborba.txt (depois de eliminadas as repetidas).
4. É fácil implementar operações como min(), max(), floor() e ceiling() em tabelas de símbolos implementadas com tabelas de hash?

Implementação 1: hashing com encadeamento

• Agora que cuidamos das funções de hashing, podemos tratar de métodos de resolução de colisões.
• Precisamos inventar um meio de resolver colisões.

  

• Resolução de colisões por encadeamento (separate chaining):  M listas ligadas, cada uma implementa uma tabela de símbolos.

  

• Em geral, N > M e portanto 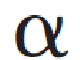> 1.
• Algoritmo 3.5: Hashing com encadeamento, classe SeparateChainingHashST (usa SequentialSearchST):

  public class SeparateChainingHashST<Key, Value> {
  
      private int N;  // número de chaves
      private int M;  // tamanho da tabela de hash
  
      private SequentialSearchST<Key,Value>[] st;  // vetor de TSs
  
      public SeparateChainingHashST(int M) {
          this.M = M;
          st = (SequentialSearchST<Key,Value>[]) new SequentialSearchST[M];
          for (int i = 0; i < M; i++)
              st[i] = new SequentialSearchST<Key,Value>();
      } 
  
      public SeparateChainingHashST() {
          this(997); // tamanho de tabela default
      } 
  
      private int hash(Key key) {
          return (key.hashCode() & 0x7fffffff) % M;
      } 
  
      public Value get(Key key) {
          int h = hash(key);
          return st[h].get(key);
      } 
  
      public void put(Key key, Value val) {
          int h = hash(key);
          st[h].put(key, val);
      } 
  

• (Com 997 listas, espera-se que esse código seja cerca de 1000 vezes mais rápido que SequentialSearchST.)
• Veja código completo em algs4/SeparateChainingHashST.java (usa redimensionamento da tabela de hash).

Análise

• O comprimento médio das listas é N/M.  Mas poderíamos ter uma lista muito longa e todas as demais muito curtas, não?  Para eliminar essa possibilidade, precisamos saber ou supor algo sobre os dados.
• Proposição K:  Em uma tabela de hash encadeada com M listas e N chaves, se vale a hipótese do hashing uniforme, a probabilidade de que o número de chaves em cada lista não passa de  N/M  multiplicado por uma pequena constante, essa probabilidade é muito próxima de 1.
• Exemplo: Se N/M = 10, a probabilidade de que uma lista tem comprimento maior que 20 é inferior a 0.8%.
• A prova da Proposição K usa apenas teoria de probabilidades clássica. Graças à hipótese do hashing uniforme, a probabilidade de que uma determinada lista tem exatamente k elementos é

         

  Resta apenas mostrar que essa distribuição binomial é bem concentrada em torno de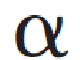 , ou seja, que a probabilidade de que a lista tenha, digamos, mais que 2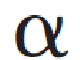 chaves é muito pequena.

• Exemplo: SW aplicou FrequencyCounter com SeparateChainingHashST de 997 listas às palavras do livro tale.txt.  No gráfico, a altura de cada barra sobre o ponto k do eixo horizontal dá o número de listas que têm comprimento k:

  

• Exemplo: SW usou o programa-cliente FrequencyCounter com SeparateChainingHashST de 997 listas para examinar as palavras com 8 ou mais letras do livro tale.txt. O gráfico mostra o número de nós visitados (= número de comparações feitas) por cada chamada de put(). Os pontos vermelhos dão a média acumulada.  (Compare com os gráficos de SequentialSearchST, BST e RedBlackBST.)

  

• Como escolher o valor de M?  Escolha M tão grande que as listas sejam curtas mas não tão grande que muitas listas fiquem vazias. Felizmente, o valor de M não é crítico.

Exercícios 4

1. Podemos ter 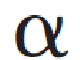< 1 numa tabela de hash com encadeamento?
2. (SW 3.4.1)  Insira as chaves  E A S Y Q U T I O N ,  nessa ordem, usando hashing com encadeamento, em uma tabela com M = 5 listas. Use a função de hashing   11*k % M   para transformar a k-ésima letra do alfabeto em um índice da tabela de hash.
3. Repita os experimentos com o livro tale.txt usando valores de M diferentes de 997 (tente valores que são potência de 2, por exemplo).
4. (SW 3.4.9)  Acrescente um método delete() à classe SeparateChainingHashST. O seu método deve ser ansioso: ele deve remover o chave solicitada imediatamente (e não simplesmente marcá-la com null para remoção posterior).
5. (SW 3.4.19)  Acrescente um iterador keys() à classe SeparateChainingHashST.
6. Acrescente um método a SeparateChainingHashST que calcule o custo médio de uma busca bem-sucedida, supondo que cada chave tem a mesma probabilidade de ser buscada. (O custo da busca é o número de comparações de chaves.)
7. Acrescente um método a SeparateChainingHashST que calcule o custo médio de uma busca malsucedida sob a hipótese de hashing uniforme. (O custo da busca é o número de comparações de chaves.)
8. (SW 3.4.36) Faixa de comprimentos de listas. Escreva um programa que insira N chaves inteiras (números int) aleatórias em uma tabela de tamanho N/100 usando hashing com encadeamento e depois determine o comprimento da lista mais curta e da mais longa. Faça isso para N igual a 10³, 10⁴, 10⁵, 10⁶.  (Faça um pequeno relatório sobre os resultados e acrescente o relatório, como comentário, ao final do seu programa.)

Implementação 2: hashing com sondagem linear

• Outro jeito de resolver colisões é a  sondagem linear (linear probing):  se uma posição da tabela estiver ocupada, tente a próxima!
• Precisamos ter N ≤ M e portanto 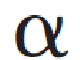≤ 1.
• Exemplo: Rastreamento de hashing com sondagem linear para as chaves  S E A R C H E X A M P L E  e tabela de hash de tamanho M = 16:

  

• Veja a animação de hashing com sondagem linear no website do livro.
• Algoritmo 3.6: Hashing com sondagem linear, classe LinearProbingHashST (sem redimensionamento):

  public class LinearProbingHashST<Key, Value> {
  
      private int N;       
      private int M = 16;  
      private Key[] keys;  
      private Value[] vals;
  
      public LinearProbingHashST() {
          keys = (Key[])   new Object[M];
          vals = (Value[]) new Object[M];
      }
  
      public LinearProbingHashST(int cap) {
          M = cap;
          keys = (Key[])   new Object[M];
          vals = (Value[]) new Object[M];
      }
  
      private int hash(Key key) {
          return (key.hashCode() & 0x7fffffff) % M;
      }
  
      public void put(Key key, Value val) {
          int i;
          for (i = hash(key); keys[i] != null; i = (i + 1) % M) 
              if (keys[i].equals(key)) { 
                  vals[i] = val; 
                  return; 
              }
          keys[i] = key;
          vals[i] = val;
          N++;
      }
  
      public Value get(Key key) {
          for (int i = hash(key); keys[i] != null; i = (i + 1) % M) 
              if (keys[i].equals(key))
                  return vals[i];
          return null;
      }
  

• Note que a tabela de hash é preenchida com null no início.
• Mantenha o fator de carga 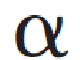sempre bem abaixo de 1.  Se N chegar perto de M, a operação de inserção pode demorar muito tempo procurando por uma posição vaga na tabela.

Análise

• Se a função de hashing satisfaz a hipótese de hashing uniforme, poderíamos pensar que as chaves ficam espalhadas por igual pela tabela. Mas não é bem assim…
• A sondagem linear tem a tendência de produzir clusters (grumos, pelotas, caroços, agrupamentos contíguos) na tabela de hash.
• Exemplo: clusters em uma tabela de hash com 64 posições:

  

• Exemplo:  padrões de ocupação de tabela de hash com sondagem linear comparada com ocupação aleatória.  (Acho que 8192 está errado; deveria ser 8191. O que você acha?):

  

• Se vale a hipótese do hashing uniforme, clusters longos tendem a crescer mais que os curtos.
• Proposição M:  Supondo que vale a hipótese do hashing uniforme, e que 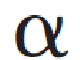está entre 0 e 1 mas não muito perto de 1,  o número médio de sondagens em buscas bem-sucedidas é aproximadamente

  

  e o número médio de sondagens em buscas malsucedidas (ou inserções) é aproximadamente

  

• Exemplo: quando 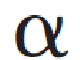= 0.5, temos aproximadamente 1.5 sondagens por busca bem-sucedida e aproximadamente 2.5 sondagens por busca malsucedida.
• Exemplo: quando 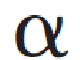= 0.25, temos aproximadamente 1.16 sondagens por busca bem-sucedida e aproximadamente 1.39 por busca malsucedida.
• Prova da Proposição M:  Knuth provou em 1962 (não é muito fácil).
• Car parking problem: Knuth faz analogia com automóveis procurando vaga de estacionamento em uma rua que já tem carros estacionados. Quantas tentativas um automóvel precisa fazer, em média?

Exercícios 5

1. Por que a análise das buscas malsucedidas e bem-sucedidas é feita em separado?
2. (SW 3.4.10)  Insira as chaves  E A S Y Q U T I O N ,  nessa ordem, usando hashing com sondagem linear, em uma tabela com M = 16 posições. Use a função de hashing   11*k % M   para transformar a k-ésima letra do alfabeto em um índice da tabela de hash.  Repita o exercício com M = 10.
3. Quero acrescentar à classe LinearProbingHashST um método delete() que remova uma dada chave key da tabela. Mostre, por meio de um exemplo simples, que o código a seguir não resolve o problema.

       public void delete(Key key) {
           if (!contains(key)) return;
           int i = hash(key);
           while (!key.equals(keys[i]))
               i = (i + 1) % M;
           keys[i] = null;
           vals[i] = null;
       }
   

4. (SW 3.4.17, p.471) Acrescente à classe LinearProbingHashST um método delete() que remova uma dada chave (e o valor associado).
5. (SW 3.4.19)  Acrescente um iterador keys() à classe LinearProbingHashST.
6. (SW 3.4.20)  Acrescente à classe LinearProbingHashST um método que calcule o custo médio de uma busca bem-sucedida, supondo que cada chave da tabela tem a mesma probabilidade de ser buscada.  (O custo da busca é o número de sondagens, ou seja, o número de posição visitadas da tabela de hash.)  Use o código de LinearProbingHashST sem redimensionamento. Escreva um cliente CustoSondagemLinear.java que teste o novo método usando um gerador de números aleatórios.  Use Visual​Accumulator para fazer um gráfico de custos em função do número N de chaves.  Superponha o gráfico com as previsões dadas na Proposição M.
7. (SW 3.4.21)  Acrescente à classe LinearProbingHashST um método que calcule o custo médio de uma busca malsucedida supondo uma função de hashing aleatória. (O custo da busca é o número de sondagens, ou seja, o número de posição visitadas da tabela de hash.)  (Observação: Não é necessário calcular nenhum função de hash para resolver essa questão.) Use o código de LinearProbingHashST sem redimensionamento. Escreva um cliente CustoSondagemLinear.java que teste o novo método usando um gerador de números aleatórios.  Use Visual​Accumulator para fazer um gráfico de custos em função do número N de chaves.  Superponha o gráfico com as previsões dadas na Proposição M.

Redimensionamento da tabela de sondagem linear

• Na sondagem linear, é essencial que 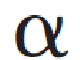fique bem abaixo de 1.  Convém manter 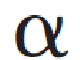≤ 1/2  (ou seja, N ≤ M/2).
• Para manter 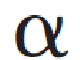sob controle, a tabela de hash deve ser redimensionada, quando necessário, no início de put().
• Algoritmo 3.6, continuação: redimensionamento em LinearProbingHashST:

      public void put(Key key, Value val) {
          if (N >= M/2) resize(2*M);
          . . . 
          . . . 
      }
  
      private void resize(int cap) {
          LinearProbingHashST<Key, Value> temp;
          temp = new LinearProbingHashST<Key, Value>(cap);
          for (int i = 0; i < M; i++) {
              if (keys[i] != null) {
                  temp.put(keys[i], vals[i]);
              }
          }
          keys = temp.keys;
          vals = temp.vals;
          M    = temp.M;
      }
  

• Também é bom manter 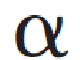> 1/8,  para evitar desperdício de espaço. Isso se faz com redimensionamento no fim de delete() quando necessário.
• Veja o código completo em algs4/​LinearProbingHashST.java.
• A troca de M por  2*M  em put() vai contra o conselho de usar números primos como valores de M.  Uma ideia melhor é usar uma tabela de primos para trocar M pelo primo imediatamente acima de 2*M.
• A análise de desempenho do hashing com redimensionamento deve ser feita, necessariamente, em termos amortizados.  A conclusão é previsível: o consumo de tempo esperado de qualquer sequência de T operações que começam com uma tabela vazia é proporcional a T.
• Exemplo: O livro aplicou FrequencyCounter com LinearProbingHashST com redimensionamento para examinar as palavras com 8 ou mais letras do livro tale.txt. O gráfico mostra o número de nós visitados (= número de comparações feitas) por cada chamada de put(). Os pontos vermelhos dão a média acumulada.

  

• Redimensionamento também pode ser aplicado ao hashing com encadeamento, mas nesse caso o redimensionamento não é essencial.
• Exemplo: O livro aplicou FrequencyCounter com SeparateChainingHashST com redimensionamento para examinar as palavras com 8 ou mais letras do livro tale.txt. O gráfico mostra o número de nós visitados (= número de comparações feitas) por cada chamada de put(). Os pontos vermelhos dão a média acumulada.

  

Exercícios 6

1. Escreva uma versão de SeparateChainingHashST que faça redimensionamento da tabela de hash.
2. (SW 3.4.26) Remoção preguiçosa sob sondagem linear. Acrescente um método delete() à classe LinearProbingHashST. Para remover uma chave da tabela, o método deve atribuir null ao valor associado à chave e adiar a efetiva remoção da chave (e do valor associado) até o momento em que a tabela for redimensionada. (Observação: Você deve sobrescrever o valor null se uma operação put() subsequente associar um novo valor à chave.) O desafio é decidir quando resize() deve ser chamado. Para tomar a decisão de redimensionar, seu método deve levar em conta não só o número de posições vagas da tabela mas também o número de posições mortas.