Esta página discute o código de Huffman. Trata-se de uma codificação de caracteres que permite compactar arquivos de texto, ou seja, representar um arquivo de texto A por um arquivo de bits B bem menor. O algoritmo de Huffman calcula uma tabela de códigos sob medida para o arquivo A de modo que o arquivo B seja o menor possível.
Começamos por apresentar e resolver um problema abstrato que, à primeira vista, não tem relação com a compactação de arquivos. No fim da página, o algoritmo para o problema abstrato é usado para resolver o problema da compactação de arquivos.
O algoritmo de Huffman é um bom exemplo de algoritmo guloso. O texto desta página é uma versão melhorada da seção 3, capítulo 16, de CLRS.
Uma árvore de Huffman é uma árvore binária em que cada nó interno tem dois filhos. Além disso, árvores de Huffman ignoram a relação de ordem (esquerdo, direito) entre os filhos de um nó. Para melhor estudar essas árvores, adotaremos uma definição mais abstrata que a usual.
Seja S um conjunto qualquer. (Você pode supor que o conjunto é { 1, 2, … , n }.) Uma árvore de Huffman com suporte S é qualquer coleção Π de subconjuntos de S que tenha as seguintes propriedades:
Os elementos de Π são chamados nós. O nó S é a raiz de Π. Os nós minimais são chamados folhas e os demais nós são internos.
Se X, Y e X ∪ Y são nós da árvore, dizemos que X e Y são os filhos de X ∪ Y. Dizemos também que X ∪ Y é o pai de X e de Y. Um ancestral de um nó X é qualquer nó I tal que I ⊇ X. Se I ⊃ X então I é ancestral próprio de X.
A profundidade de um nó X é o número de ancestrais próprios de X. (A profundidade da raiz, por exemplo, é 0.) A profundidade de um nó X será denotada por d(X).
Toda árvore de Huffman com mais de dois nós tem pelo menos duas folhas X e Y tais que X ∪ Y também é um nó; dizemos que X e Y são folhas irmãs. Se X e Y são folhas irmãs de uma árvore de Huffman Π então Π − {X, Y} também é uma árvore de Huffman.
O conjunto de todas as folhas de uma árvore de Huffman é uma partição do suporte S. Reciprocamente, dada qualquer partição Γ de S, existe pelo menos uma árvore de Huffman que tem Γ como conjunto de folhas.
Diremos que uma árvore de Huffman tem folhas unitárias se cada uma de suas folhas tem cardinalidade 1. Em outras palavras, a árvore tem folhas unitárias se cada uma de suas folhas tem a forma {s} para algum s em S.
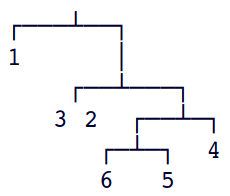
Exemplo A. A coleção {{1}, {2, 3}, {4}, {5}, {6}, {5, 6}, {4, 5, 6}, {2, 3, 4, 5, 6}, {1, 2, 3, 4, 5, 6}} é uma árvore de Huffman com suporte {1, 2, 3, 4, 5, 6}. As folhas da árvore são {1}, {2, 3}, {4}, {5} e {6}. O nó {4, 5, 6} é pai dos nós {4} e {5, 6}. As folhas {5} e {6} são irmãs; ambas têm profundidade 4. Essa árvore pode ser representada graficamente assim:
Uma ponderação de um conjunto S é uma atribuição de pesos numéricos aos elementos de S. Dada uma ponderação (pi : i ∈ S) e um subconjunto X de S, denotaremos por p(X) a soma ∑i∈X pi . Diremos que p(X) é o peso de X.
Suponha que Π é uma árvore de Huffman e (pi : i ∈ S) uma ponderação do suporte S de Π. O peso de Π, denotado por p(Π), é a soma dos pesos de todos os nós exceto a raiz. (Com essa definição, uma expressão da forma p( ) passa a ter duas interpretações diferentes, conforme seu argumento seja uma árvore de Huffman ou um subconjunto do suporte da árvore.) Portanto,
p(Π) = ∑X ∈ Π−{S} p(X) .
O peso de Π pode ser calculado a partir dos pesos de suas folhas: se Γ é o conjunto das folhas de Π e d(F) a profundidade de uma folha F então
| p(Π) = ∑F ∈ Γ p(F) d(F) . | (*) |
Problema central. Agora que temos o conceito de peso, podemos apresentar o problema central desta página. A solução desse problema é a peça central do algoritmo a compressão ótima de um arquivo de caracteres, a ser discutida na última seção desta página.
Problema da árvore de Huffman de peso mínimo: Dada uma partição Γ de um conjunto S e uma ponderação de S, encontrar uma árvore de Huffman de peso mínimo dentre as que têm conjunto de folhas Γ.
Uma árvore de Huffman Π é ótima em relação a uma ponderação p se p(Π) ≤ p(Π′) para toda árvore de Huffman Π′ que tenha o mesmo conjunto de folhas que Π. Nosso problema é, portanto, encontrar uma árvore de Huffman ótima dentre as que têm um dado conjunto de folhas. (Estamos especialmente interessados no conjunto de folhas unitárias.)
O problema da árvore de Huffman de peso mínimo tem uma propriedade estrutural simples e natural. Sejam X e Y duas folhas irmãs de uma árvore de Huffman Π. Seja Π′ a árvore de Huffman Π − {X, Y} e observe que Π e Π′ têm o mesmo suporte.
Propriedade recursiva: Se Π é ótima para uma ponderação p do suporte então Π′ também é ótima.
Prova: Seja Γ o conjunto de folhas de Π. Então Γ′ = (Γ − {X,Y}) ∪ {X∪Y} é o conjunto de folhas de Π′. Suponha, por um momento, que Π′ não é ótima. Então existe uma árvore de Huffman Φ′ com conjunto de folhas Γ′ tal que p(Φ′) < p(Π′). A coleção Φ = Φ′ ∪ {X, Y} é uma árvore Huffman com conjunto de folhas Γ. Observe que
| p(Φ) | = | p(Φ′) + p(X) + p(Y) |
| < | p(Π′) + p(X) + p(Y) | |
| = | p(Π) . |
A desigualdade p(Φ) < p(Π) contradiz a suposta otimalidade de Π. A contradição mostra que Π′ é, de fato, ótima, CQD.
A recíproca da propriedade também vale: Suponha que U é uma folha de uma árvore de Huffman Π′ e que {X, Y} é uma bipartição de U tal que X e Y não são vazios. Se Π′ é ótima então a árvore de Huffman Π = Π′ ∪ {X, Y} também é ótima.
Para qualquer instância do problema da árvore de Huffman de peso mínimo, existe uma árvore ótima em que as duas folhas mais leves são também as mais profundas. Esta é a propriedade que leva a um algoritmo guloso para o problema.
Para formular a propriedade tornar de maneira precisa, seja p uma ponderação do suporte S, seja Γ uma partição de S, e sejam X e Y dois elementos de Γ. Então vale a seguinte
Propriedade gulosa: Se p(X) ≤ p(Y) ≤ p(V) para todo V em Γ − {X, Y} então existe uma árvore de Huffman ótima com conjunto Γ de folhas na qual X e Y são folhas irmãs de profundidade máxima.
Prova: Seja Π uma árvore de Huffman ótima com conjunto Γ de folhas. Seja V uma folha de profundidade máxima. Então V é irmã de alguma outra folha, digamos W. É claro que V eW têm a mesma profundidade. Se d( ) denota a profundidade de um nó, podemos dizer que d(V) = d(W). Como V tem profundidade máxima, temos d(V) ≥ d(X) e d(W) ≥ d(Y). Ajuste a notação (trocando os papéis de V e W se necessário) de modo que p(V) ≤ p(W). Teremos então
p(X) ≤ p(V) e p(Y) ≤ p(W) .
Agora troque X e V de posição em Π, produzindo assim uma árvore de Huffman Π′. Mais precisamente, Π′ é definida assim:
Observe que Π′ é, de fato, uma árvore de Huffman e que seu conjunto de folhas é Γ. Denote por d′( ) as profundidades em Π′ e observe que d′(X) = d(V) e d′(V) = d(X). Ademais, d′(Z) = d(Z) para toda folha Z distinta de X e V. De acordo com a equação (*) na seção Árvores de Huffman de peso mínimo,
| p(Π) − p(Π′) = | ||
| = | ∑F∈Γ p(F) d(F) − ∑F∈Γ p(F) d′(F) | |
| = | p(X) d(X) + p(V) d(V) − p(X) d′(X) − p(V) d′(V) | |
| = | p(X) d(X) + p(V) d(V) − p(X) d(V) − p(V) d(X) | |
| = | (p(V) − p(X)) (d(V) − d(X)) | |
| ≥ | 0 . | |
Portanto, a árvore de Huffman Π′ é tão ótima quanto Π. Ademais, X é uma folha de profundidade máxima em Π′.
Agora troque Y e W de posição em Π′ produzindo assim uma árvore de Huffman Π″ com conjunto Γ de folhas. Um argumento análogo ao aplicado a X e V mostra que Π″ também é ótima. Finalmente, observe que em Π″ as folhas X e Y são irmãs e têm profundidade máxima.
David Huffman inventou (1952)
um algoritmo muito eficiente para o problema da árvore de Huffman de peso mínimo.
(É claro que o nome árvore de Huffman
só veio depois!)
O algoritmo de Huffman tem caráter guloso e decorre da propriedade gulosa e da estrutura recursiva discutidas acima.
Ao receber uma ponderação p do suporte S e uma partição Γ de S, o algoritmo devolve uma árvore de Huffman ótima com conjunto Γ de folhas:
| 1Huffman (p, Γ) |
| 11 . se ⎮Γ⎮ = 1 |
| 12 .ooo devolva Γ e pare |
| 13 . seja X um elemento de Γ que minimiza p(X) |
| 14 . Γ := Γ − {X} |
| 15 . seja Y um elemento de Γ que minimiza p(Y) |
| 16 . Γ := Γ − {Y} |
| 17 . Γ := Γ ∪ {X ∪ Y} |
| 18 . Π := Huffman (p, Γ) |
| 19 . devolva Π ∪ {X, Y} |
Na linha 2, é claro que o único elemento de Γ é S. Na linha 8, o conjunto Γ é menor que o da linha 3, e portanto a instância do problema submetida a Huffman é menor que a instância original.
A prova da correção do algoritmo está na propriedade gulosa e na recíproca da estrutura recursiva discutidas acima.
Exemplo B. Suponha que S = { 1, 2, … , n } e considere a ponderação dada pela tabela a seguir. (Note que os pesos estão em ordem decrescente.)
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| pi | 45 | 13 | 12 | 16 | 9 | 5 |
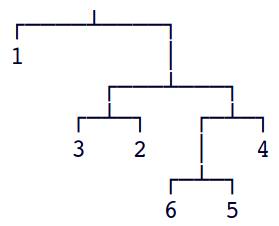
(O exemplo foi copiado da página 389 do CLRS.) Seja Γ a partição unitária do suporte S. Com esses parâmetros, o algoritmo de Huffman produz a árvore de Huffman {{1}, {2}, {3}, {4}, {5}, {6}, {6, 5}, {6, 5, 4}, {2, 3}, {2, 3, 4, 5, 6}, {1, 2, 3, 4, 5, 6}}. A maneira como essa árvore é construída é bem representada pelo seguinte diagrama:
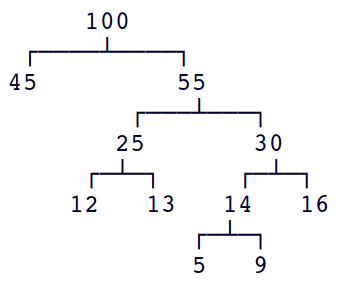
A árvore poderia também ser representada pela expressão (1, ((3, 2), ((6, 5), 4))). Um diagrama ainda mais sugestivo indica o peso de cada nó:
Essa árvore de Huffman tem peso 224. Para contrastar, considere a árvore de Huffman ((1, 2), ((5, 6), (3, 4))), que tem peso 242 e portanto não é ótima.
É natural usar uma árvore binária usual como estrutura de dados para representar uma árvore de Huffman. Para uma implementação não recursiva do algoritmo de Huffman, basta representar árvores de Huffman com folhas unitárias.
Cada nó da árvore de Huffman será representado por uma célula dotada de quatro campos: esq, dir, índice e p. Para cada célula z, esq[z] é o endereço do filho esquerdo de z e dir[z] é o endereço do filho direito de z. Se z representa uma folha então esq[z] = dir[z] = nil. Se z não representa uma folha então índice[z] é irrelevante. Se z representa uma folha { i } então índice[z] = i. Para cada z, p[z] é o peso do nó da árvore que a célula z representa.
Podemos agora reescrever o algoritmo de Huffman em estilo iterativo. Vamos supor que o conjunto-suporte S é { 1, 2, … , n }. O algoritmo recebe uma ponderação p de S e devolve o endereço da raiz de uma árvore binária que representa uma árvore de Huffman ótima com folhas unitárias.
| 1Huffman (n, p) |
| 11 . Q := Nova-Fila-com-Prioridades ( ) |
| 12 . para i crescendo de 1 até n |
| 13 .ooo z := Cria-Célula ( ) |
| 14 .ooo índice[z] := i |
| 15 .ooo p[z] := pi |
| 16 .ooo esq[z] := dir[z] := nil |
| 17 .ooo Insere-na-Fila (Q, z) |
| 18 . enquanto Q tiver 2 ou mais células |
| 19 .ooo x := Extrai-Min (Q) |
| 10 .ooo y := Extrai-Min (Q) |
| 11 .ooo z := Cria-Célula ( ) |
| 12 .ooo esq[z] := x |
| 13 .ooo dir[z] := y |
| 14 .ooo p[z] := p[x] + p[y] |
| 15 .ooo Insere-na-Fila (Q, z) |
| 16 . r := Extrai-Min (Q) |
| 17 . devolva r |
A operação Nova-Fila-com-Prioridades () cria uma fila-com-prioridades vazia. Os elementos da fila serão células e a prioridade de cada célula z é p[z]. A operação Cria-Célula gera uma nova célula e devolve o endereço dessa célula. A operação Insere-na-Fila (Q, z) insere a célula z na fila Q.
As linhas 1 a 7 constroem as folhas da árvore. As demais linhas constroem os nós internos e a estrutura da árvore. A operação Extrai-Min (Q) nas linhas 9 e 10 retira da fila-com-prioridades Q uma célula que tem p mínimo.
No início de cada iteração temos uma floresta composta de duas ou mais árvores. (No início da primeira iteração, cada árvore tem apenas um nó.) Durante a iteração, o algoritmo escolhe duas raízes e funde as correspondentes árvores. No fim da última iteração, a floresta tem uma única árvore.
O invariante principal do algoritmo é o seguinte: no início de cada iteração do bloco de linhas 9 a 15,
a floresta faz parte de alguma árvore ótima.
A prova do invariante segue da propriedade gulosa e da recíproca da estrutura recursiva discutidas acima.
Desempenho. Quanto tempo o algoritmo Huffman consome? Se a fila-com-prioridades for implementada como um vetor ordenado, cada execução de Insere-na-Fila e Extrai-Min consumirá Ο(m) unidades de tempo, sendo m o número de células na fila Q. Como m ≤ n e há n repetições do bloco de linhas 1 a 7 e n−1 repetições do bloco de linhas 9 a 15, o consumo de tempo total do algoritmo será Ο(n2).
Se a fila-com-prioridades for implementada como um min-heap (veja um dos exercícios abaixo), cada execução de Insere-na-Fila e Extrai-Min consumirá Ο(lg n) unidades de tempo. Com isso, o consumo total será de
Ο(n lg n)
unidades de tempo.
vetorpor
lista encadeadaou por
arquivose desejar.) Digamos que Ai tem pi elementos. Suponha dado um algoritmo Merge que recebe dois vetores Ai e Aj e consome pi + pj unidades de tempo para produzir um vetor B que é o resultado da intercalação de Ai e Aj. (É claro que o vetor B estará em ordem crescente e conterá pi + pj números.) Queremos usar Merge para intercalar todos os vetores dados, produzindo assim um único vetor em ordem crescente, no menor tempo possível. Quantas vezes será necessário invocar Merge? Em que ordem os vetores devem ser submetidos ao Merge para que a soma dos tempos do Merge seja mínima? (Compare com exercício semelhante na página sobre filas-com-prioridades.)
A principal aplicação prática do algoritmo de Huffman é o cálculo de códigos binários para compressão de arquivos, ou seja, a transformação de um arquivo de caracteres em uma sequência de bits que ocupa pouco espaço. (Veja o verbete Huffman coding na Wikipedia.) A ideia é usar poucos bits para representar os caracteres mais frequentes e mais bits para representar os mais raros.
Uma tabela de códigos para um conjunto C de caracteres é uma bijeção entre C e algum conjunto de sequências de bits. A sequência de bits que corresponde a um dado caractere é o código do caractere.
Uma tabela de códigos é livre de prefixos (= prefix-free) (= prefix-free) se tem a seguinte propriedade: para quaisquer dois caracteres x e y, o código de x não é prefixo do código de y. (Um prefixo de um sequência de bits b1, b2, … , bk é qualquer segmento inicial b1, b2, … , bi com i ≤ k.)
| A | 0 |
| B | 101 |
| C | 100 |
| D | 111 |
| E | 1101 |
| F | 1100 |
Exemplo C. A figura à direita mostra uma tabela de códigos para o conjunto de caracteres {A, B, … , F}. (O exemplo foi extraído da página 386 do CLRS.) A tabela é livre de prefixos. Para essa tabela, a sequência de caracteres ABACAFE é representada pela sequência de bits 01010100011001101. Nenhuma outra sequência de caracteres é representada por essa sequência de bits.
Um arquivo (= file) é uma sequência de caracteres. O conjunto de caracteres do arquivo é o alfabeto do arquivo. O peso de um caractere c num arquivo é a frequência de c, ou seja, o número de ocorrências de c no arquivo. O peso de um caractere c será denotada por p(c). Assim, o número de caracteres do arquivo é igual a ∑c∈C p(c).
Dada uma tabela de códigos para o alfabeto de um arquivo, a codificação do arquivo é a substituição de cada caractere pelo correspondente código. Durante a codificação, os códigos dos caracteres são simplesmente concatenados, sem quaisquer separadores, de modo que o arquivo codificado é uma longa sequência de bits. Se a tabela de códigos for livre de prefixos, a codificação não introduz ambiguidades, pois a sequência de bits só pode ser decodificada de uma maneira.
O comprimento (= length) do arquivo codificado é o número total de bits do arquivo. Temos, então, o seguinte
Problema de compressão: Dado um arquivo de caracteres, encontrar uma tabela de códigos que produza um arquivo codificado de comprimento mínimo.
Vamos restringir nossa atenção às tabelas de códigos que podem ser representadas por árvores de códigos. Uma árvore de códigos para um conjunto C de caracteres é uma árvore binária em que
O código de um caractere c é dado pelo caminho que vai da raiz da árvore até c: cada vez que o caminho vai de um nó interno para seu filho esquerdo temos um bit 0 e cada vez que o caminho vai para o filho direito temos um bit 1. É claro que o número de bits do código de c é igual à profundidade de c na árvore. É claro também que a tabela de códigos assim obtida é livre de prefixos.
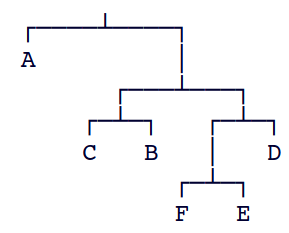
Exemplo D. A tabela do exemplo C pode ser representada pela seguinte árvore:
Para decodificar uma sequência de bits, basta percorrer a árvore a partir da raiz usando a sequência como guia. Comece na raiz da árvore; para cada bit 0, vá para a esquerda; para cada bit 1, vá para a direita; continue até atingir uma folha.
Para cada caractere c, denotaremos por d(c) a profundidade de c na árvore. É claro que d(c) é também o comprimento (ou seja, o número de bits) do código de c. O número total de bits do arquivo codificado é então
∑c∈C d(c) p(c) ,
sendo p(c) o peso de c no arquivo. Como vimos acima, esta soma é igual ao peso da árvore de Huffman que corresponde à árvore de códigos. (Para obter a árvore de Huffman, basta ignorar a distinção entre filho esquerdo e filho direito de cada nó interno da árvore de códigos.)
Nosso problema de compressão de arquivos se reduz, assim, ao problema da árvore de Huffman de peso mínimo. O algoritmo de Huffman pode ser usado, portanto, para comprimir arquivos.
| a | b | c | d | e | f |
| 00 | 010 | 0110 | 0111 | 10 | 11 |