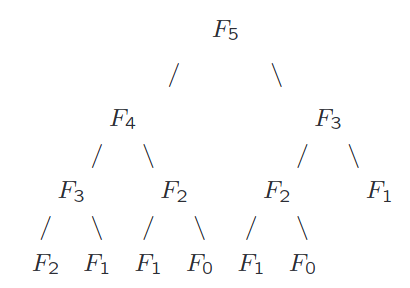
Dynamic programming is a fancy name for
[recursion]
with a table.
Instead of solving subproblems recursively,
solve them sequentially and store their solutions in a table.
The trick is to solve them in the right order
so that whenever the solution to a subproblem is needed,
it is already available in the table.
— Ian Parberry, Problems on Algorithms
Muitos algoritmos eficientes
são baseados no método de programação dinâmica
(= dynamic programming).
Esse método, ou estratégia de projeto de algoritmos,
é uma espécie de tradução iterativa inteligente da recursão
e pode ser definido, vagamente,
como recursão com o apoio de uma tabela
.
Como em um algoritmo recursivo, cada instância do problema é resolvida a partir da solução de instâncias menores, ou melhor, de subinstâncias da instância original. A característica distintiva da programação dinâmica é a tabela que armazena as soluções das várias subinstâncias. O consumo de tempo do algoritmo é, em geral, proporcional ao tamanho da tabela.
(A palavra programação na expressão
programação dinâmica
não tem relação direta com
programação de computadores.
Ela significa planejamento
e refere-se à construção da tabela
que armazena
as soluções das subinstâncias.
A propósito, veja a
resposta de Shai Simonson à pergunta
What does the "Dynamic" mean in Dynamic Programming?
no Quora.)
Para que o método da programação dinâmica possa ser aplicado,
é preciso que o problema tenha estrutura recursiva:
a solução de toda instância do problema deve conter
soluções de subinstâncias da instância.
(O livro de CLRS diz optimal substructure
.)
Essa estrutura recursiva é
representada por uma recorrência,
e a recorrência pode ser traduzida em um algoritmo recursivo.
Em alguns casos, o algoritmo recursivo
refaz a solução de cada subinstância muitas vezes,
e isso torna o algoritmo ineficiente.
Nesses casos,
é possível armazenar as solução das subinstância numa tabela
e assim evitar que elas sejam recalculadas.
Considere a célebre sequência 0, 1, 1, 2, 3, 5, 8, … de números de Fibonacci. (Veja exercício na página Recorrências.) Esses números são definidos pela recorrência F(n) = F(n − 1) + F(n − 2) a partir dos valores iniciais F(0) = 0 e F(1) = 1.
Nosso problema é calcular F(n)
dado n.
O seguinte algoritmo resolve o problema
de cima para baixo
,
em estilo recursivo:
| Fib (n) |
| 1 . se n ≤ 1 |
| 2 .ooo devolva n e pare |
| 3 . devolva Fib (n − 1) + Fib (n − 2) |
Este algoritmo é muito ineficiente pois recalcula F(i) várias vezes para cada i, como a figura abaixo sugere. (É um excelente exercício mostrar que o algoritmo Fib consome Ω(1.5 n) unidades de tempo.)
Para evitar que cada F(i) seja recalculado várias vezes,
podemos empregar o método de programação dinâmica.
(Note que o problema tem estrutura recursiva,
representada pela recorrência que define os números de Fibonacci.)
O algoritmo abaixo usa uma tabela f [0 .. n]
para armazenar os números de Fibonacci à medida que são calculados,
de baixo para cima
:
| Fib-PD (n) |
| 1 . f [0] := 0 |
| 2 . f [1] := 1 |
| 3 . para i := 2 até n |
| 4 .ooo f [i] := f [i − 1] + f [i − 2] |
| 5 . devolva f[n] |
Esse algoritmo consome apenas Θ(n) unidades de tempo.
condições iniciaisda recorrência.) Mostre também que o algoritmo consome Ο(1.7 n) unidades de tempo.
Eis alguns algoritmos que usam o método de programação dinâmica: