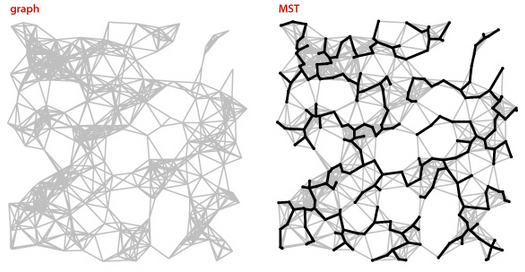
Esta página trata do problema das árvores geradoras de peso mínimo em grafos. Trata-se de uma generalização do problema da árvore geradora discutido no capítulo Árvores geradoras de grafos. Esse problema é mais conhecido pelas iniciais MST de minimum spanning tree. A página trata, em particular, do célebre algoritmo de Kruskal para o problema da MST.
Esta página é inspirada no capítulo 23 do livro CLRS.
Suponha que cada aresta uv de um grafo tem um peso p[uv]. Cada peso é um número positivo, negativo, ou nulo. Vamos supor que os pesos são inteiros (embora isso não seja essencial). Diremos que p é um vetor de pesos. O peso de um subgrafo T do grafo é a soma dos pesos das arestas de T e será denotado por p(T).
Exemplo A. A tabela abaixo atribui um peso p[a] a cada aresta a do grafo da figura. (Neste exemplo, o peso de cada aresta é proporcional ao comprimento geométrico do segmento de reta que representa a aresta na figura.)
| a] | 4 5 | 4 7 | 5 7 | 0 7 | 1 5 | 0 4 | 2 3 | 1 7 | 0 2 | 1 2 | 1 3 | 2 7 | 6 2 | 3 6 | 6 0 | 6 4 |
| p[a] | 35 | 37 | 28 | 16 | 32 | 38 | 17 | 19 | 26 | 36 | 29 | 34 | 40 | 52 | 58 | 93 |
O conjunto de arestas 0 7 7 1 7 5 5 4 0 2 2 3 2 6 define uma árvore geradora do grafo. O peso dessa árvore é 35 + 28 + 16 + 17 + 19 + 26 + 40 = 181. Nenhuma outra árvore geradora tem peso menor (mas isso não é óbvio).
Uma MST (= minimum spanning tree) de um grafo com vetor de pesos p é uma árvore geradora T do grafo que minimiza p(T).
Problema da MST: Dado um grafo G com pesos inteiros arbitrários nas arestas, encontrar uma MST de G.
É claro que uma instância do problema tem solução se e somente se G é conexo, ou seja, se cada vértice de G estiver ao alcance de cada um dos demais.
J. Kruskal descobriu (1956) um algoritmo muito eficiente para o problema da MST. O algoritmo de Kruskal é iterativo. Cada iteração começa com uma floresta geradora F de G. A cada iteração, o algoritmo acrescenta a F uma aresta de G. O critério de escolha da nova aresta é guloso: o algoritmo escolhe uma aresta de peso mínimo dentre as que são externas à floresta. Uma aresta a é considerada externa a F se satisfaz duas condições naturais e óbvias: (1) não pertence a F e (2) o grafo F + a é uma floresta. O algoritmo pode, então, ser resumido assim:
| enquanto existem arestas externas, |
| .oo escolha uma aresta externa de peso mínimo, |
| .oo seja uv a aresta escolhida, |
| .oo troque F por F + uv. |
No início da primeira iteração, a floresta F não tem aresta alguma (e o conjunto de vértices de F é V(G)). No início da última iteração, G não tem arestas externas a F.
No fim da execução do algoritmo, a floresta F será conexa desde que o grafo G seja conexo. Sob essa hipótese, F será uma MST, como mostraremos mais abaixo.
Exemplo B. O vídeo Kruskal's Algorithm Animation no YouTube aplica o algoritmo de Kruskal a um grafo cujos vértices são pontos aleatórios no plano. O grafo é completo, ou seja, todo par de vértices é uma aresta. O peso de cada aresta é a distância geométrica entre suas pontas.
Exemplo C. Considere o problema de encontrar uma MST no grafo com pesos nas arestas definido a seguir. As arestas são apresentadas em ordem crescente de peso.
53 71 76 20 07 01 43 54 74 06 46 05 0 1 2 3 4 5 6 7 8 9 9 11
Veja o rastreamento da execução do algoritmo de Kruskal. Cada linha da tabela registra as arestas da floresta F e o peso p(F) da floresta no início de uma iteração.
- 0 53 0 53 71 1 53 71 76 3 53 71 76 20 6 53 71 76 20 07 10 53 71 76 20 07 43 16 53 71 76 20 07 43 74 24
A última linha dá as arestas de uma MST.
Prova da correção do algoritmo. Vamos supor que o grafo G é conexo. Para mostrar que o algoritmo de Kruskal está correto, basta provar o seguinte invariante do processo iterativo: no início de cada iteração,
| F é subgrafo de alguma MST de G. | (*) |
Essa proposição é obviamente verdadeira no início da primeira iteração, quando F não tem aresta alguma. Suponha agora que estamos no início de alguma iteração (exceto a última) e que F faz parte de uma MST M. Seja uv a aresta que o algoritmo escolhe nessa iteração. Precisamos provar que a floresta F + uv faz parte alguma MST.
Como uv é externa a F, uma das pontas de uv está em uma componente de F e a outra ponta está em outra componente. Seja U o conjunto de vértices de uma dessas componentes.
Agora considere a relação entre uv e M. Se uv é aresta de M, nada mais temos a provar. Suponha agora que uv não é aresta de M e seja C o único caminho de u a v em M. Alguma aresta xy de C tem uma ponta em U e outra ponta em . Segue daí que xy não pertence a F e F + xy é uma floresta, donde xy é externa a F. Como xy não foi escolhida durante a iteração corrente, temos p(xy) ≥ p(uv). Observe agora que
é uma árvore geradora. O peso dessa nova árvore não é maior que o peso de M. Logo, a nova árvore geradora é uma MST. Essa nova MST contém F + uv. Era o que queríamos provar.
o algoritmo faz isso, depois faz aquilo …, etc.)?
Para implementar o algoritmo de Kruskal, é preciso inventar uma maneira eficiente de decidir se uma dada aresta de G é externa a F. É claro que uma aresta é externa a F se e somente se tem uma ponta em uma componente de F e a outra ponta em outra componente. Isso sugere que o tipo abstrato de dados union-find (veja o capítulo A estrutura union-find) pode ser útil.
O algoritmo MST-Kruskal abaixo recebe um grafo conexo G com n vértices, m arestas, e um peso inteiro arbitrário p[uv] para cada aresta uv. O algoritmo devolve uma MST de G.
| MST-Kruskal (G, n, m, p) |
| 11 . arestas := Sort-Edges (G, m, p) |
| 12 . X := { } |
| 13 . Initialize () |
| 14 . para i := 1 até m |
| 15 .ooo uv := arestas[i] |
| 16 .ooo r := Find (u) |
| 17 .ooo s := Find (v) |
| 18 .ooo se r ≠ s |
| 19 .oooooo X := X ∪ { uv } |
| 10 .oooooo Union (r, s) |
| 11 . devolva (V(G), X) |
O algoritmo auxiliar Sort-Edges recebe um grafo G com m arestas e um peso p[uv] para cada aresta uv e devolve um vetor arestas[1 .. m] que contém todas as arestas em ordem crescente de pesos.
No início de cada iteração, X é o conjunto de arestas de uma floresta geradora, que chamaremos F. Os algoritmos auxiliares Find e Union atuam sobre as componentes de F:
diretorda componente de F a que esse vértice pertence;
diretoresr e s de duas componente de F, faz a fusão das duas componentes, e designa r ou s como
diretorda nova componente;
diretoressobre a qual Find e Union operam.
Desempenho do algoritmo. Vamos supor que as implementações de Initialize, Find e Union usam a heurística union-by-rank. Então Initialize consome Ο(n) unidades de tempo, cada execução de Find consome Ο(lg n) e cada execução de Union consome Ο(1) unidades de tempo. Com isso, o bloco de linhas 2-10 do algoritmo MST-Kruskal consome Ο(n + m lg n) unidades de tempo.
A linha 1 do algoritmo consome Ο(m lg m) unidades de tempo. Como m < n², podemos dizer que a linha 1 consome Ο(m lg n) unidades de tempo. Assim, o consumo de tempo total de MST-Kruskal está em
Ο(n + m lg n) .
Poderíamos lançar mão das implementações de Initialize, Find e Union que usam a heurística path compression (além da heurística union-by-rank). Com isso, o bloco de linhas 2-10 do algoritmo MST-Kruskal consumiria apenas Ο(n + m log* n) unidades de tempo, em termos amortizados. Mas o consumo de tempo total do algoritmo continuaria em Ο(n + m lg n) por conta da linha 1, que rearranja as arestas em ordem crescente de peso.
-representando
∞.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | - | 3 | - | 4 | 5 | - | - | - |
| 2 | 3 | - | 9 | - | 6 | - | - | - |
| 3 | - | 9 | - | - | 8 | 2 | - | - |
| 4 | 4 | - | - | - | 6 | - | 6 | 7 |
| 5 | 5 | 6 | 8 | 6 | - | 9 | - | 8 |
| 6 | - | - | 2 | - | 9 | - | - | - |
| 7 | - | - | - | 6 | - | - | - | 8 |
| 8 | - | - | - | 7 | 8 | - | 8 | - |