Next: About this document ... Up: Testando o viés analítico Previous: Modelo funcional homocedástico com
Em muitas situações práticas as variâncias de ambas as medidas são diferentes para cada nível de concentração. Nesta seção estudaremos o modelo funcional heterocedástico com erros nas variáveis, descrevendo as principais características do modelo e quais suposições são necessárias para utilizar tal modelo. A distribuição conjunta de (![]() ) é dada por
) é dada por
as variáveis ![]() e
e ![]() têm a mesma interpretação que no caso homocedástico,
têm a mesma interpretação que no caso homocedástico, ![]() é o viés aditivo e
é o viés aditivo e ![]() o viés multiplicativo,
o viés multiplicativo, ![]() e
e ![]() são variâncias conhecidas de
são variâncias conhecidas de ![]() e
e ![]() para
para
![]() respectivamente. Assim o logarítmo da função de verossimilhança é dada por
respectivamente. Assim o logarítmo da função de verossimilhança é dada por
sendo
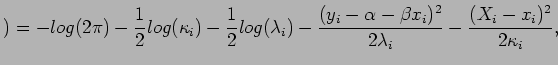
e o parâmetro
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]() e
e
![]()
![]() . A log-verossimilhança (
. A log-verossimilhança (![]() ) é limitada, pois as variâncias são conhecidas. Ripley e Thompson (1987) consideram o modelo heterocedástico acima e derivam os estimadores para
) é limitada, pois as variâncias são conhecidas. Ripley e Thompson (1987) consideram o modelo heterocedástico acima e derivam os estimadores para ![]() e
e ![]() , a partir da verossimilhança perfilada que se obtém substituindo
, a partir da verossimilhança perfilada que se obtém substituindo ![]() por
por
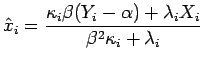 , pois
, pois ![]() maximiza (
maximiza (![]() ) em relação a
) em relação a ![]() . Os autores também propuseram testes marginais para
. Os autores também propuseram testes marginais para ![]() e
e ![]() , sendo que as variâncias usadas para o teste são obtidas por analogia a metodologia de mínimos quadrados, que não são consistentes assintóticamente. Em Galea et al 2003 encontram estimativas consistentes para a matriz de covariâncias de
, sendo que as variâncias usadas para o teste são obtidas por analogia a metodologia de mínimos quadrados, que não são consistentes assintóticamente. Em Galea et al 2003 encontram estimativas consistentes para a matriz de covariâncias de
![]() e
e
![]() baseadas na teoria de estimação para parâmetros incidentais, ver Mak, usando a verossimilhança perfilada. Os autores demonstram que as estimativas para
baseadas na teoria de estimação para parâmetros incidentais, ver Mak, usando a verossimilhança perfilada. Os autores demonstram que as estimativas para ![]() e
e ![]() são
são
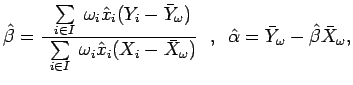
sendo que
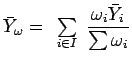 ,
, 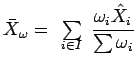
e
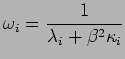 ,
,
Para se obter as estimativas de máxima verossimilhança faz-se necessário um método iterativo. O algoritmo proposto pelos autores segue os seguintes passos: (1) Inicia-se o procedimento iterativo com ![]() e os valores iniciais
e os valores iniciais
![]() ,
, ![]() , (2) calcule
, (2) calcule
![]() , (3) calcule
, (3) calcule
![]() e
e
![]() , (4) incremente uma unidade a
, (4) incremente uma unidade a ![]() , (5) repita os passos 2, 3 e 4 até a convergência. A matriz de covariâncias assintótica para os estimadores é obtida calculando
, (5) repita os passos 2, 3 e 4 até a convergência. A matriz de covariâncias assintótica para os estimadores é obtida calculando
![\begin{displaymath}(\hat{\mbox{\boldmath {$\beta$}}})=1/n W^{-1}VW^{-1}=
\left[
...
...sigma_{\beta \alpha} & \sigma_{\beta \beta}
\end{array}\right],\end{displaymath}](img99.png)
sendo que
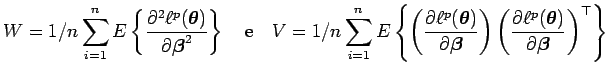
Galea et al 2003 mostram que os elementos da matriz de covariâncias assintótica de
![]() são
são
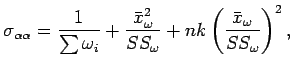
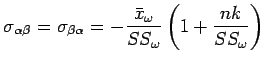 e
e
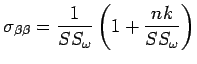
sendo que
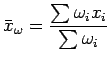 e
e
Para estimar
Var![]() consistentemente, basta substituir
consistentemente, basta substituir ![]() ,
, ![]() ,
, ![]() e
e ![]() por
por
![]() ,
,
![]() ,
, ![]() e
e
![]() , respectivamente que são as estimativas obtidas no último passo do processo iterativo. A estimativa para
, respectivamente que são as estimativas obtidas no último passo do processo iterativo. A estimativa para ![]() é dada por
é dada por
![]() . De forma analoga ao caso homocedástico, é possível usar a estatística de Wald para testar se o método novo mensura sem viés a concentração desejada.
. De forma analoga ao caso homocedástico, é possível usar a estatística de Wald para testar se o método novo mensura sem viés a concentração desejada.
Os modelos acima podem ser estendidos para o caso em que existem vários métodos a serem validados. Galea et al 2003 também derivam os estimadores para este caso, usando a verossimilhança perfilada, e propõe uma estatística de Wald para testar o viés dos métodos.
patriota 2006-04-16