Next: Modelo funcional heterocedástico com Up: Testando o viés analítico Previous: Testando o viés analítico
Existem duas abordagens em modelos com erro nas variáveis, ou seja, o modelo funcional que não supõem uma distribuição para a verdadeira concentração, e o modelo estrutural que considera uma distribuição para a verdadeira concentração. Neste trabalho consideramos apenas o modelo funcional por ser menos restritivo em relação a distribuição da concentração, podendo a mesma ser assimétrica. Essa abordagem gera alguns problemas na consistência dos estimadores pois algumas condições de regularidade não estão satistifeitas. Ema dessas condições é que o número de parâmetros cresce com o tamanho da amostra, ou seja, o modelo considera que
![]() são parâmetros incidentais. Considerando que os erros de medição seguem uma distribuição normal, o modelo funcional homocedástico é dado por
são parâmetros incidentais. Considerando que os erros de medição seguem uma distribuição normal, o modelo funcional homocedástico é dado por
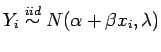
e
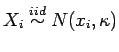
de modo que a distribuição conjunta de (![]() ) é dada por
) é dada por
![$\displaystyle \left( \begin{array}{c} Y_i\\ X_i \end{array} \right) \sim N_2\le...
...t[ \begin{array}{cc} \lambda & 0 \\ \cdot & \kappa \end{array} \right] \right),$](img5.png) |
para
![]() , sendo
, sendo
![]() Valor observado da
Valor observado da ![]() -ésima concentração medida pelo método novo;
-ésima concentração medida pelo método novo;
![]() Valor observado da
Valor observado da ![]() -ésima concentração medida pelo método padrão;
-ésima concentração medida pelo método padrão;
![]() Valor verdadeiro da
Valor verdadeiro da ![]() -ésima concentração (não observado);
-ésima concentração (não observado);
![]() Viés aditivo do modelo;
Viés aditivo do modelo;
![]() Viés multiplicativo do modelo.
Viés multiplicativo do modelo.
Neste modelo ![]() é o valor da
é o valor da ![]() -ésima concentração observada pelo instrumento novo que pode possuir alguma vantagem em relação ao instrumento padrão, como por exemplo custos mais baixos, maior facilidade na manipulação do equipamento (métodos, instrumentos) de medição, menor tempo de treinamento para que uma pessoa o opere, entre outros. A variável
-ésima concentração observada pelo instrumento novo que pode possuir alguma vantagem em relação ao instrumento padrão, como por exemplo custos mais baixos, maior facilidade na manipulação do equipamento (métodos, instrumentos) de medição, menor tempo de treinamento para que uma pessoa o opere, entre outros. A variável ![]() é o valor observado da
é o valor observado da ![]() -ésima concentração medida pelo método padrão, o instrumento padrão mensura a concentração com grande precisão, mas com algum custo operacional não desejado. O interesse principal é verificar se o método novo consegue mensurar sem viés a concentração desejada, para isso utilizamos a metodologia da máxima verossimilhança, sendo o loarítmo da função de verossimilhança dado por
-ésima concentração medida pelo método padrão, o instrumento padrão mensura a concentração com grande precisão, mas com algum custo operacional não desejado. O interesse principal é verificar se o método novo consegue mensurar sem viés a concentração desejada, para isso utilizamos a metodologia da máxima verossimilhança, sendo o loarítmo da função de verossimilhança dado por
sendo
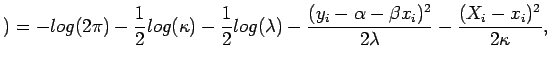
e o parâmetro
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]() e
e
![]()
![]() . Portanto, temos
. Portanto, temos ![]() parâmetros para serem estimados. Uma das formas de obter estimadores consistentes para o viés aditivo
parâmetros para serem estimados. Uma das formas de obter estimadores consistentes para o viés aditivo ![]() e para o viés multiplicativo
e para o viés multiplicativo ![]() é maximizar a log-verossimilhança perfilada, ou seja substituir
é maximizar a log-verossimilhança perfilada, ou seja substituir ![]() pelo seu estimador de máxima verossimilhança (MV) dado por
pelo seu estimador de máxima verossimilhança (MV) dado por ![]() em (
em (![]() ) obtendo
) obtendo
sendo
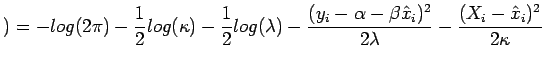
e
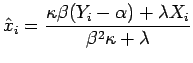 . Além desse problema verifica-se que a verossimilhança acima é ilimitada, gerando problemas de maximização, quando
. Além desse problema verifica-se que a verossimilhança acima é ilimitada, gerando problemas de maximização, quando
![]() e
e
![]() . Uma das formas de contornar este problema é considerar conhecido alguns parâmetros. Quando consideramos
. Uma das formas de contornar este problema é considerar conhecido alguns parâmetros. Quando consideramos
![]() conhecido, (substituindo
conhecido, (substituindo ![]() por
por
![]() ) a log-verossimilhança se torna limitada, porém o estimador de MV para
) a log-verossimilhança se torna limitada, porém o estimador de MV para ![]() não é consistente, ver Patefield 1978, um estimador consistente para
não é consistente, ver Patefield 1978, um estimador consistente para ![]() é dado por
é dado por
![]() sendo que
sendo que
![]() é o estimador de MV. Patefield 1978 mostra que os estimadores para
é o estimador de MV. Patefield 1978 mostra que os estimadores para ![]() ,
, ![]() e
e ![]() para o caso em que
para o caso em que ![]() é conhecido são dados por
é conhecido são dados por
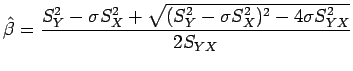 e
e
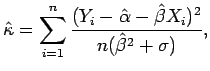
os quais serão consistentes se
sendo ![]() e
e ![]() constantes. Patefield 1977 deriva as variâncias assintóticas dos estimadores
constantes. Patefield 1977 deriva as variâncias assintóticas dos estimadores
![]() e
e
![]() no caso ultraestrutural, ou seja, quando a verdadeira concentração
no caso ultraestrutural, ou seja, quando a verdadeira concentração ![]() tem distribuição normal com média
tem distribuição normal com média ![]() e variância
e variância
![]() . Fazendo
. Fazendo
![]() , temos como caso particular o modelo funcional. O estimador consistente para a matriz de covariâncias é dado abaixo
, temos como caso particular o modelo funcional. O estimador consistente para a matriz de covariâncias é dado abaixo
![\begin{displaymath}\hat{\mbox{Var}}(\hat{\mbox{\boldmath {$\beta$}}})=
\dfrac{(\...
...\
-\bar{X}(1+\hat{\tau}) & (1+ \hat{\tau})
\end{array}\right]
\end{displaymath}](img59.png)
sendo
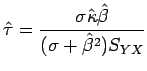 ,
,
![]() e
e
![]() .
.
Assim é possível utilizar a estatística de Wald para testar
![]() contra
contra
![]() , ou seja, testar se não existe viés aditivo (
, ou seja, testar se não existe viés aditivo (![]() ) e multiplicativo (
) e multiplicativo (![]() ) na medição do intrumento novo. A estatística Wald para este caso é dada por
) na medição do intrumento novo. A estatística Wald para este caso é dada por
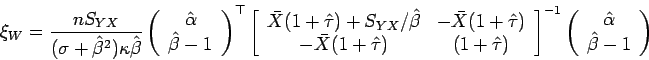
Pelas propriedades dos estimadores obtidos maximizando a log-verossimilhança perfilada, ver Mak, pode-se mostrar que a distribuição assintótica de ![]() é uma quiquadrado com 2 graus de liberdade. Quando consideramos
é uma quiquadrado com 2 graus de liberdade. Quando consideramos ![]() conhecido a log-verossimilhança perfilada se torna limitada, mas o estimador de MV para
conhecido a log-verossimilhança perfilada se torna limitada, mas o estimador de MV para ![]() não é consistente, (ver Fuller), assim o estimador de MV para o caso estrutural é usado para estimar
não é consistente, (ver Fuller), assim o estimador de MV para o caso estrutural é usado para estimar ![]() ( ver Cheng e Van Ness 1991). Estimadores consistentes para
( ver Cheng e Van Ness 1991). Estimadores consistentes para ![]() ,
, ![]() e
e ![]() , quando
, quando ![]() é conhecido, são dados por
é conhecido, são dados por
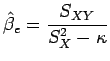 e
e
Cheng e Van Ness 1991 encontram a matriz de covariâncias assintótica de
![]() que é dada por
que é dada por
![\begin{displaymath}\hat{\mbox{Var}}(\hat{\mbox{\boldmath {$\beta$}}})=1/n
\left[...
...{\psi} \\
-\bar{X}\hat{\psi} & \hat{\psi}
\end{array}\right]
\end{displaymath}](img72.png)
sendo
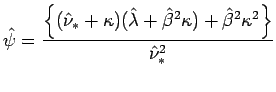 e
e
![]() . Desta forma para testar se não existe viés no instrumento novo poderiamos utilizar a estatística de Wald de forma analoga ao caso em que
. Desta forma para testar se não existe viés no instrumento novo poderiamos utilizar a estatística de Wald de forma analoga ao caso em que
![]() é conhecido. A estatística é dada por
é conhecido. A estatística é dada por
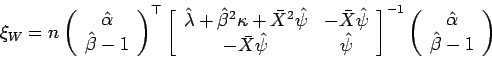
Poderiamos também considerar ![]() e
e ![]() conhecidos, assim os parâmetros
conhecidos, assim os parâmetros ![]() e
e ![]() são estimados consistentemente, fazendo
são estimados consistentemente, fazendo
![]() . Os estimadores encontrados usando a verossimilhança perfilada do viés aditivo e multiplicativo são dados por
. Os estimadores encontrados usando a verossimilhança perfilada do viés aditivo e multiplicativo são dados por
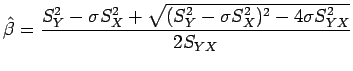
que coincidem com o caso em que apenas ![]() é conhecido. A matriz de covâriancias assintótica de
é conhecido. A matriz de covâriancias assintótica de
![]() no caso em que ambas as variâncias são conhecidas é
no caso em que ambas as variâncias são conhecidas é
![\begin{displaymath}
\hat{\mbox{Var}}(\hat{\mbox{\boldmath {$\beta$}}})=1/n
\left...
...\psi} \\
-\bar{X}\hat{\psi} & \hat{\psi}
\end{array}\right],
\end{displaymath}](img76.png)
sendo
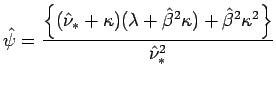 e
e
![]() . A estatística Wald para testar o viés é dada abaixo
. A estatística Wald para testar o viés é dada abaixo
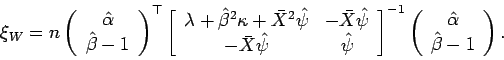
A distribuição assintótica da estatística acima é quiquadrado com 2 graus de liberdade. (colocar aqui a referencia do Singer, 1993)
patriota 2006-04-16