.: Interesting points in triangle: some examples :.
In this section are presented some intriguing geometric constructions associated to triangles with iGeom.
The interesting property is related to 3 lines concurrent in a single point.
To understand the intriguing points, we need the concept of cevian line.
Given any triangle ABC, a cevian line of this triangle, is a line passing by any vertex of the triangle and intercepting its opposite side (or its extension)
[Coxeter, Greitzer, 1967].
In the figure below the line rA is cevian, since it pass by the vertex A and cross the opposite side (to A) BC.
The intriguing points examined in this section occurs whenever the 3 cevian line has a single point in common.
Note that, 3 concurrent lines can have 3 points in common, each one common to a pair of theses lines.
| Cevian lines: considering rA, rB, and rC the lines passing by the points
A, B, and C, respectively; |
| consider the points pA, pB, and pC, respectively, the points over the sides BC, AC, and AB; |
if the intersection betwee the 3 pairs of cevian lines rA, rB, and rC is a single point,
then this is an intriguing point
(Ceva's theorem presents a condition to the existence of this point - see
[Coxeter, Greitzer, 1967] or
WikiPedia).
|
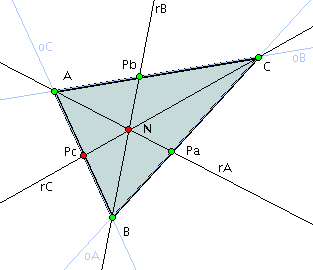
Fig. Ilustration of an intriguing point N generated by the cevian lines rA, rB, and rC
To see the page, please, "click" over the "links" below.
The circumcenter
of a triangle ABC is the (unique) intersection point of the three perpendicular bissectors of the triangle.
Any perpendicular bissector is not itself a cevian lines, however, each one has an associated cevian line:
the line passing by any vertex and the midpoint in its opposite side (note that it is the intersection of the perpendicular bissector and the opposite side).
The centroid
of a triangle ABC is the (unique) intersection point of the three medians of the triangle.
In this case, the cevian is precisely the median line (the line formed the vertex and the midpoint at the opposite side).
The orthocenter
of a triangle ABC is the (unique) intersection point of the three altitudes of the triangle's vertex.
In the orthocenter, the cevians are the altitudes of each vertex (therefore, associated with the line passing by each vertex and orthogonal to the opposite side).
The Gergonne point
of a triangle ABC is the (unique) intersection point formed by the cevian lines defined by the intersections
of the inscribed circumference with the opposite side AB, AC, and BC.
[Coxeter, Greitzer, 1967] H. S. M. Coxeter, S. L. Greitzer, Geometry Revisited, MAA, 1967.
Italian mathematician Giovanni Ceva, who published in 1678 a condition (sine qua non) to the existence of this single point, the Ceva's theorem.
