.: Circumcenter of a Triangle (remarkable point) :.
Circumcenter of a Triangle (remarkable point):
Given any three non-collinear points A, B, and C, the triangle circumcenter of ABC
is the point G that is the (unique) intersection point of the triangle perpendicular lines.
In this case, the perpendicular bissector must be constructed considering each one the triangle sides.
Since there are 3 perpendicular bissectors, they can be taken 2-by-2 (pA with pB; pA with pC; e pB with pC), resulting in 3 possible intersections.
However, these 3 possible instersction points is reduced to a single point! It is remarkable, isn't it?
remarkable point
An remarkable Point of a triangle is the point resulting of the intersection of three lines
that passes through each triangle vertex and its opposite side (cevian lines).
The remarkable fact is the existence of a single point, since there are 3 possible intersections
(one to each pair of lines)!
These lines is named as cevians in honor the mathematician Giovanni Ceva (that published a condition to existence of this single point in 1678).
See: H. S. M. Coxeter, S. L. Greitzer, Geometry Revisited, MAA, 1967.
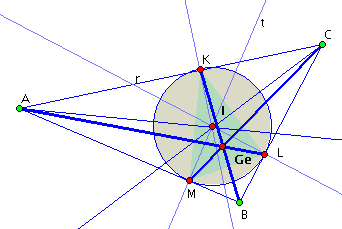
Fig.: static figure representing the Gergonne (note that I is the incenter) point (an special "remarkable point").
Interactive construction with iGeom
Below is presented the Circumcenter of a (generic) Triangle in iGeom.
Hands on: try to move the point A (B or C) and observe that:
the segments AL, BK, and CM
has a common point Ge as its intersection (Gergonne point).
In order to move any point (the best) option is: with the "move button"
selected (a single right "click" on it), make a right "click" over
the target point (this means "click" and release the mouse button), then
freely move the mouse around the drawing area.
.