
|
|
CapXIV-pg9 |
|
Seria interessante saber se todo modelo poligonal de uma superfície com bordo é homeomorfo a algum modelo poligonal com buracos. |
Veremos que isso é verdade usando o próprio exemplo do Cilindro (ou do Anel, como queira). É fácil ver que o método é aplicável em qualquer superfície, desde que alguns cuidados sejam tomados. |
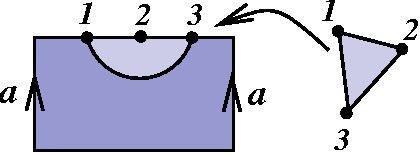
Para começar, definimos uma triangulação no Cilindro, respeitando algumas exigências. Primeiro, todo par de vértices deve estar ligado por apenas uma aresta. Veja abaixo uma situação proibida, onde os vértices 1 e 2, ou os vértices 1 e 3, estão ligados por duas arestas. |

|
Segundo, cada triângulo deve ter no máximo uma aresta no bordo. Veja abaixo o que seria um triângulo com duas arestas no bordo. |
|
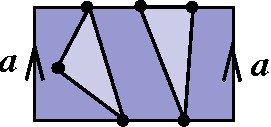
Terceiro, um triângulo só pode encostar em no máximo um segmento do bordo. Enconstar aqui significa ter um vértice ou uma aresta no bordo. No exemplo abaixo, proibido por essa regra, os dois triângulos sombreados encostam nas duas componentes de bordo do cilindro. |
|
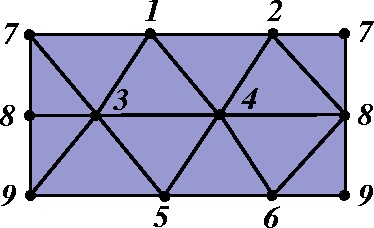
Observe que a triangulação abaixo respeita as três exigências. |
|
Agora destacamos as componentes de bordo. |

|
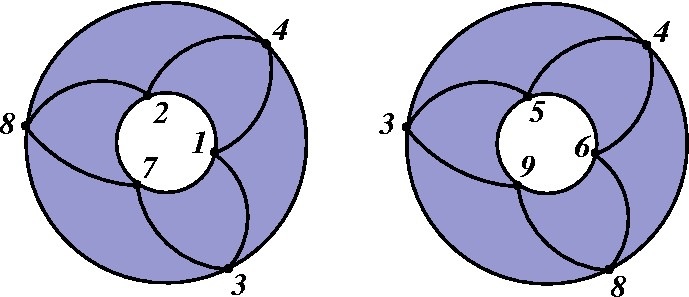
Depois colamos um a um os triângulos que encostam nos respectivos bordos. |
|
As duas componentes de bordo ficam cercadas, cada uma dentro de um disco. Então colamos os discos. |
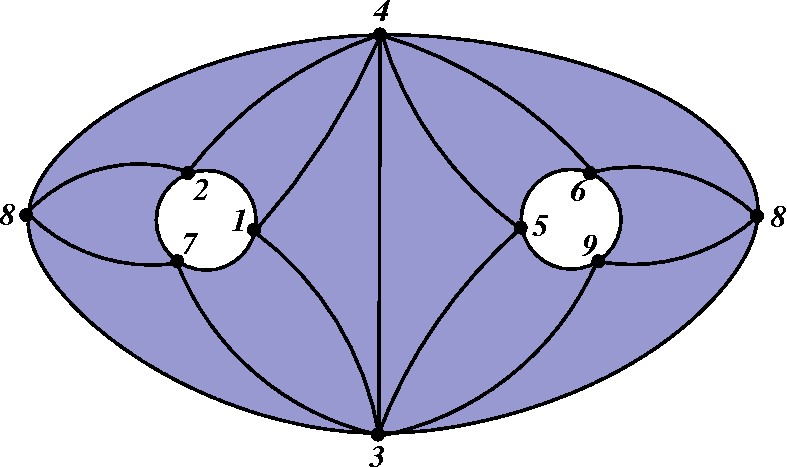
|
O resultado é um modelo poligonal com buracos. |
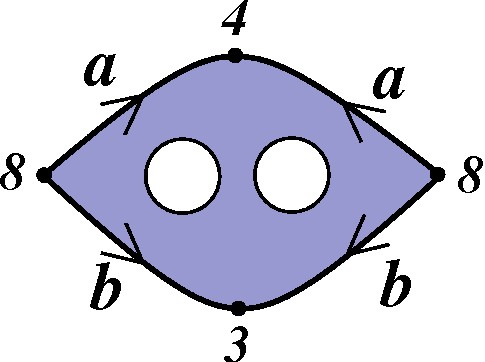
|
Colando as arestas etiquetadas com a letra "a", simplificamos o modelo, obtendo o que desejávamos: uma Esfera de onde removemos duas tampas. |
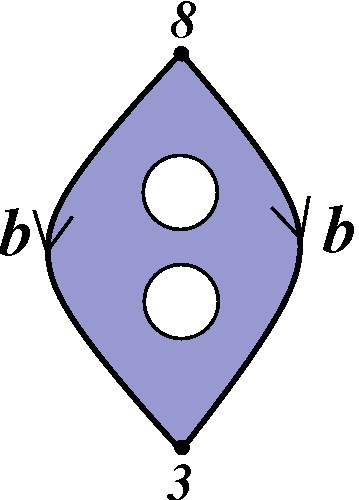
|
Como dissemos, esse procedimento sempre pode ser feito em superfícies com bordo. Ou seja, toda superfície com bordo admite um modelo poligonal com buracos, tal que se tamparmos os buracos, obteremos um modelo poligonal de uma superfície sem bordo. |
Portanto a partir daqui nos concentraremos apenas em modelos poligonais de superfícies sem bordo. |
|
CapXIV-pg9 |
|