|
|
CapXIV-pg8 |
|
Há um modo fácil de ver que toda superfície admite
um modelo poligonal. A "receita" é a seguinte:
|
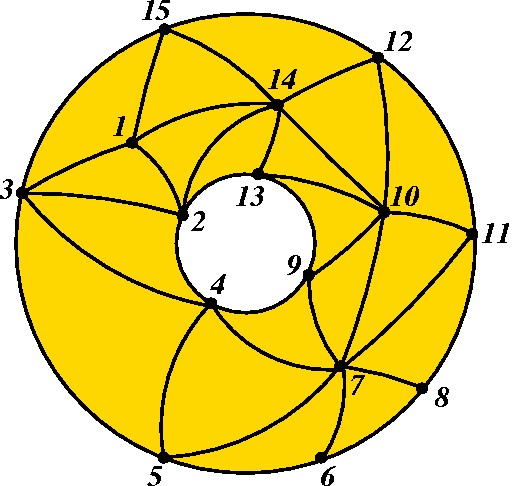
Ilustremos a receita com um exemplo simples: o anel. |
Etapa 1. Triangulação com numeração dos vértices. |

|
Etapa 2. Recorte dos triângulos (com retificação de formato). |
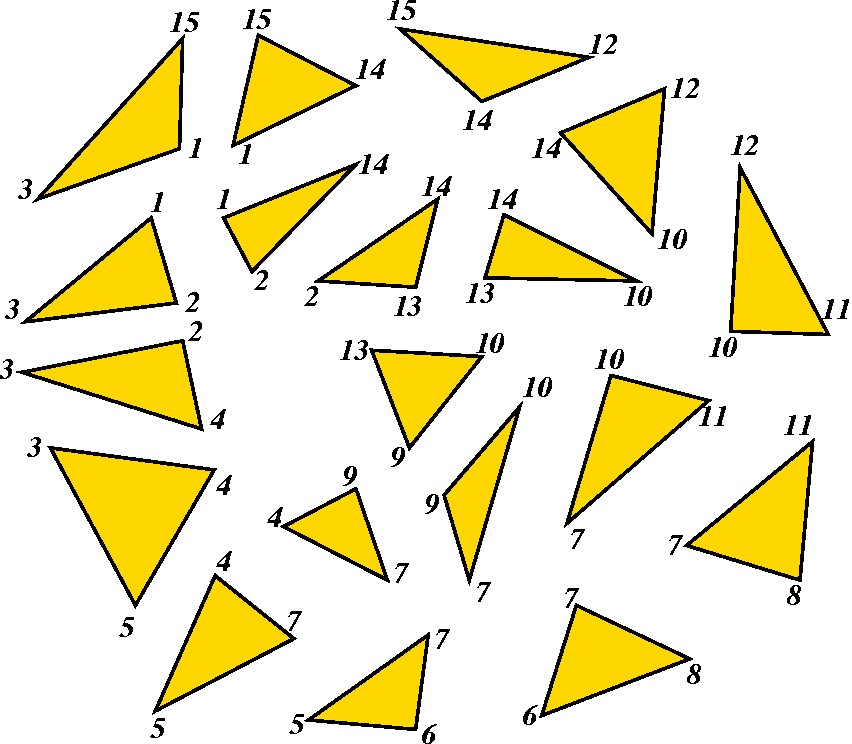
|
Etapa 3. Colagem. Nesta etapa, começa-se com um triângulo qualquer, por exemplo: |
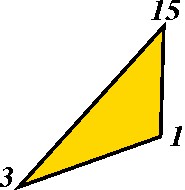
|
Os outros triângulos são agregados um a um, sempre mantendo-se um pedaço coeso. Além disso, impõe-se a regra de que cada triângulo novo só seja colado por um lado. |
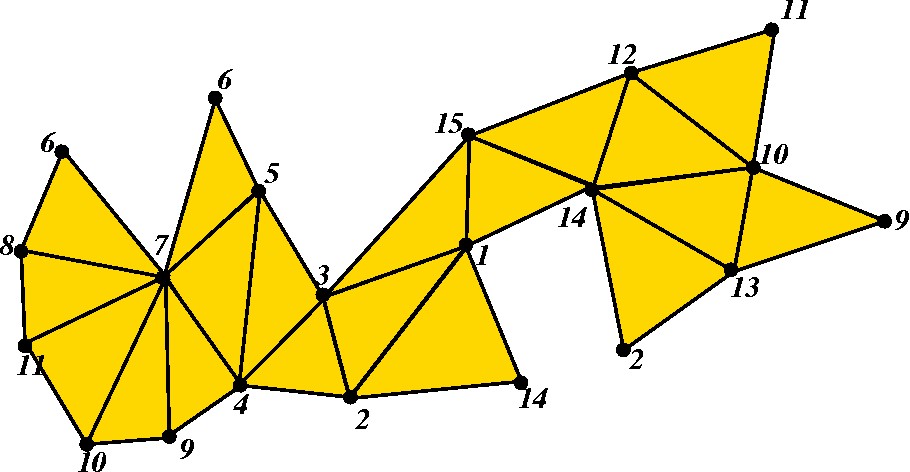
|
Dessa forma, a figura toda é sempre isotópica a um disco e o resultado final é um polígono, cujo bordo é demarcado pelos vértices numerados. |
O próximo passo é arrumar o polígono, mantendo-se a numeração dos vértices de bordo. |
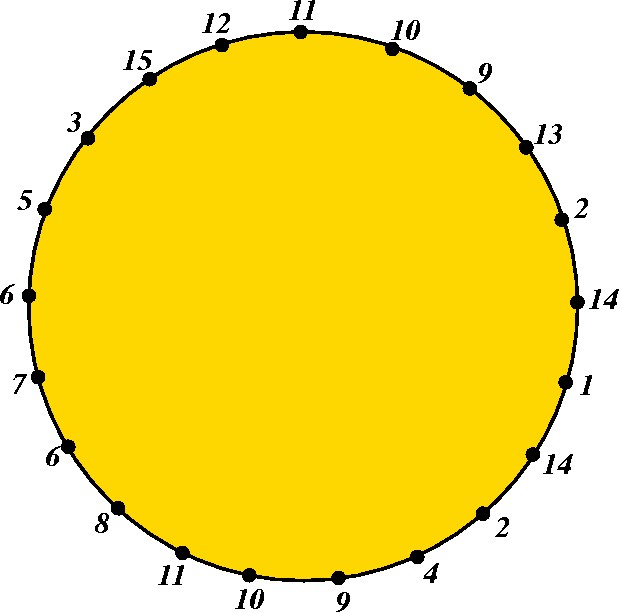
|
Etapa 4. A cada aresta associa-se uma letra. Lados a serem identificados (ou seja, que têm os mesmos números nas pontas) recebem letras iguais, respeitando-se a orientação, definida por esses mesmos números. Por exemplo, escolhemos a letra a para o segmento que liga os vértices 10 e 11, e o sentido vai de 11 para 10. Já os lados solitários não recebem orientação e são etiquetados com a letra "B". |
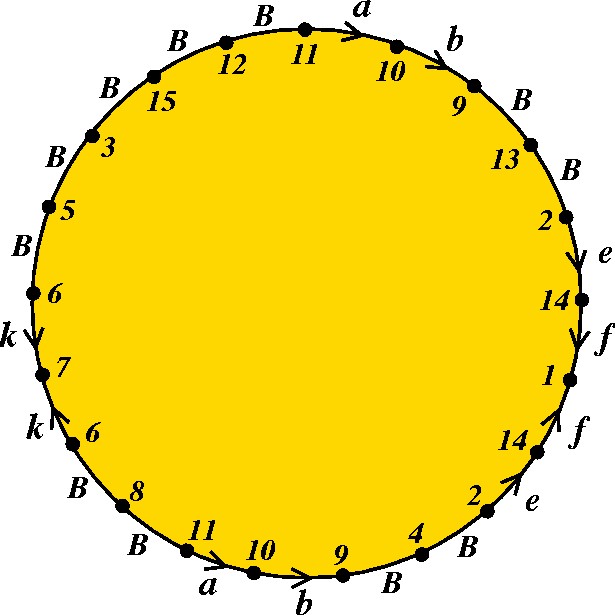
|
Pronto! Obtivemos um modelo poligonal para o Anel! Em letras, ele é dado por: abBBeff-1e-1BBb-1a-1BBkk-1BBBBB. E não é difícil ver que o mesmo pode ser feito com qualquer superfície, desde que consigamos obter uma triangulação. |
É evidente, no entanto, que esse não é o modelo mais simples para o Anel. Lembremos que o Anel é isotópico ao Cilindro, e portanto o modelo do Cilindro é o mais apropriado, como mostra a figura abaixo. |

|
O que podemos fazer, entretanto, é simplificar o modelo que obtivemos, com alguns pequenos truques. Essa simplificação não vai alterar a superfície, mas sim o modelo. Por exemplo, podemos começar juntando todos os segmentos de bordo adjacentes: o modelo fica, em letras, dado por abBeff-1e-1Bb-1a-1Bkk-1B, que corresponde à seguinte figura: |
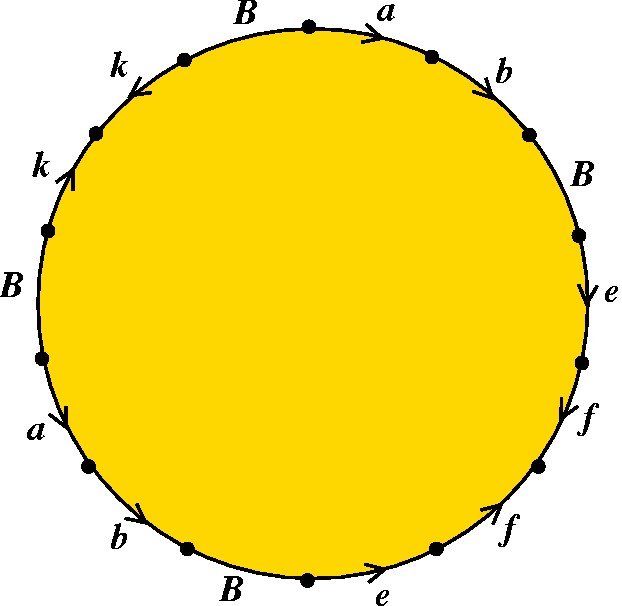
|
Além disso, os segmentos a e b podem ser colados simultaneamente, o que permite juntar os dois segmentos sob uma mesma letra: c. O mesmo ocorre com e e f, que juntaremos na letra d. O modelo fica mais simplificado ainda: cBdd-1Bc-1Bkk-1B, como na ilustração abaixo. |
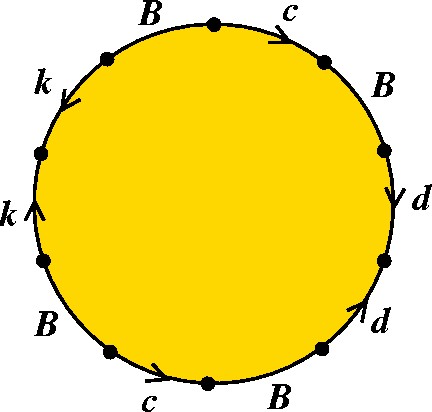
|
Outra simplificação: quando um par de segmentos com a mesma letra é adjacente, e os sentidos das setas são opostos, podemos colá-los, como indica a figura abaixo com respeito às letras d e k. Esses segmentos desaparecem do contorno do polígono. |
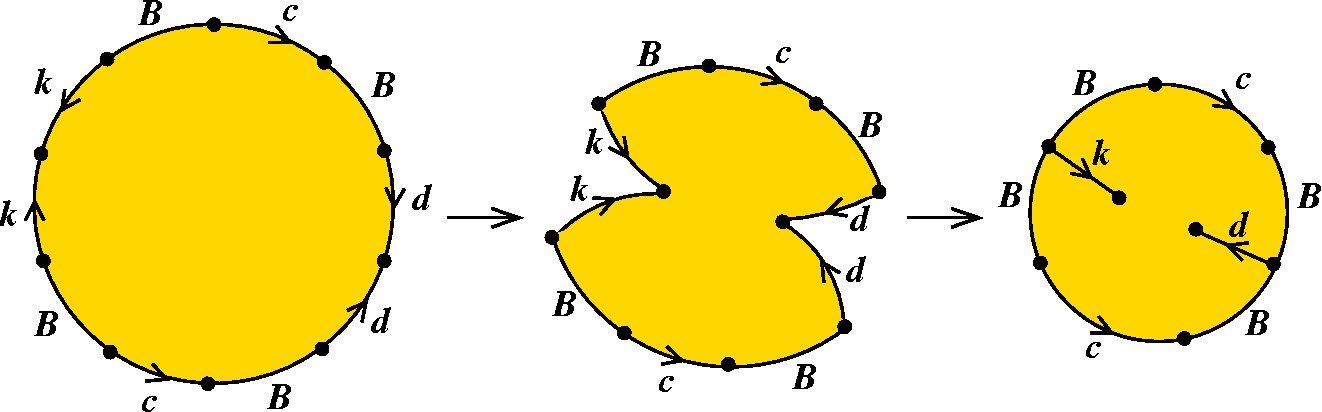
|
Agora há mais segmentos de bordos adjacentes, que podem ser juntados, resultando em: |
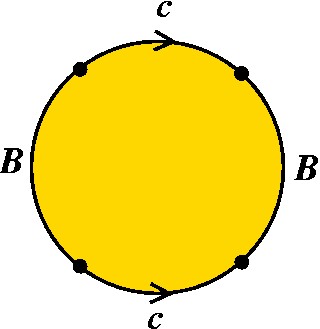
|
Ora, esse é exatamente o modelo do Cilindro e do Anel! (Só que nesta figura desenhamos um "retângulo redondo"!) |
Por outro lado, podemos considerar outro tipo de modelo para a mesma superfície: ele leva em conta que o Cilindro é uma Esfera sem duas tampas, e poderia ser representado assim: |
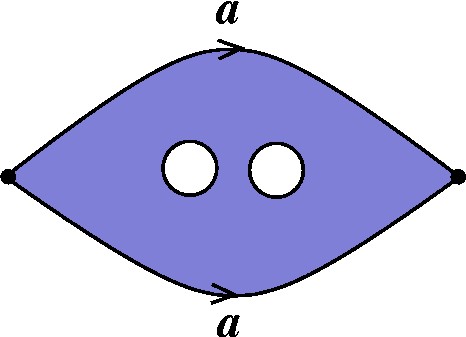
|
Isso não é exatamente um modelo poligonal, pois há buracos no meio (lembre-se que polígonos são isotópicos a discos, de acordo com nossa definição). No entanto esse modelo é bem mais conveniente para superfícies com bordo, pois revela de qual superfície sem bordo elas derivam e quantas componentes de bordo elas têm. |
Chamaremos esse tipo de modelo de modelo poligonal com buracos. |
|
CapXIV-pg8 |
|