|
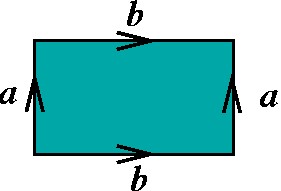
Toro: aba-1b-1 |
|
|
CapXIV-pg7 |
|
Existe uma maneira muito simples de se definir um modelo poligonal sem desenhá-lo. |
A idéia é convencionar um sentido para percorrer o bordo do polígono, por exemplo, o sentido horário, e então escrever as letras de cada lado, na ordem em que aparecem. Se a orientação de um lado for oposta ao sentido que percorremos, colocamos então um índice -1 sobre a letra correspondente. O lado que começamos é arbitrário. Os lados que correspondem a pedaços do bordo recebem a letra "B", mas deve-se lembrar que eles não devem ser identificados! |
Por exemplo, dentre os modelos que discutimos... |
|
Toro: aba-1b-1 |

|
|
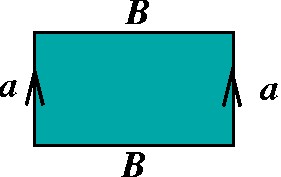
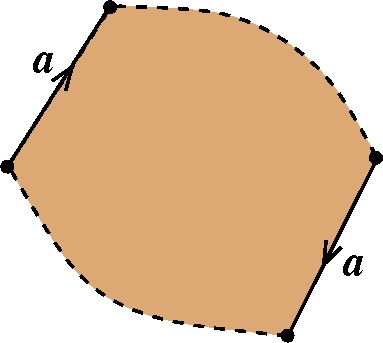
Cilindro: aBa-1B |
|
|
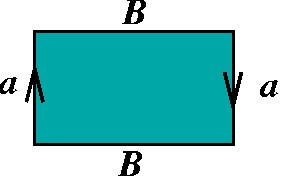
Moebius: aBaB |
|
|
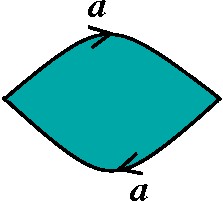
Plano Projetivo: aa |
|
|
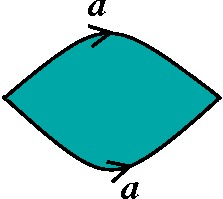
Esfera: aa-1 |
|
|
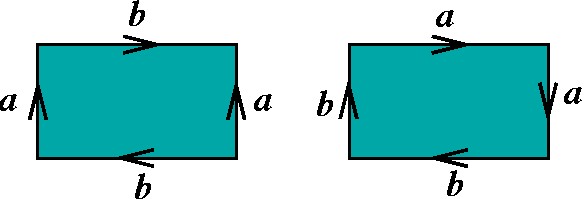
Klein: aba-1b ou aabb |
|
|
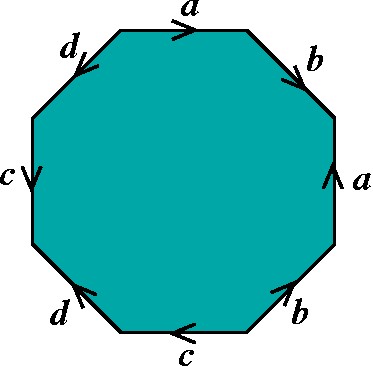
Bitoro: aba-1b-1cdc-1d-1 |
|
|
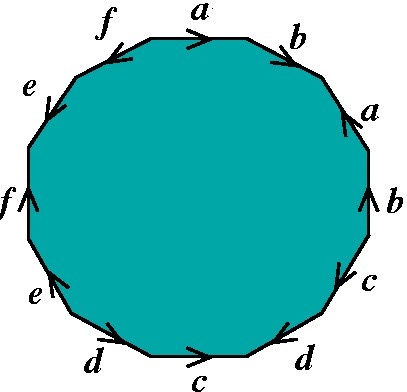
Tritoro: aba-1b-1cdc-1d-1efe-1f-1 |
|
Então, somar um Toro a uma superfície é o mesmo que acrescentar uma seqüência "aba-1b-1" ao seu modelo. Já somar um Plano Projetivo é o mesmo que acrescentar uma seqüência do tipo "aa" ao modelo. |
É importante notar que, se algum par de letras aparece em sentidos iguais no modelo, então a superfície é não-orientável. |
|
Basta ver que as antenas de Aderbal "trocam de lado" quando passam pelo segmento a. Antes de iniciar sua caminhada, Aderbal está com as antenas alinhadas de acordo com seu "holograma", mas quando volta elas estão ao contrário! |
Ou seja, Aderbal nos mostra que existe um caminho desorientador, que consiste em atravessar o lado a uma vez. Observe que se o par de letras a estivesse orientado em sentidos opostos esse caminho não seria desorientador! |
Concluímos então que se todos os pares de letras estão em sentidos opostos então a superfície é orientável, pois não há nenhum caminho desorientador que Aderbal possa percorrer! |
|
CapXIV-pg7 |
|