|
|
CapXIV-pg10 |
|
Modelos poligonais de superfícies sem bordo |
Se uma superfície não tem bordo, seu modelo poligonal não pode ter lados "solitários": todas as letras devem ocorrer aos pares. Daí decorre que o modelo poligonal só pode ter um número par de lados: 2, 4, 6, 8, etc. |
Chamaremos de modelo poligonal pareado a qualquer modelo poligonal que não tenha arestas solitárias. É claro que também não permitiremos mais do que dois lados etiquetados com a mesma letra. |
Uma pergunta natural: "todo modelo poligonal pareado define uma superfície?" |
Para responder a essa pergunta, devemos recorrer à noção de vizinhança. É preciso saber se todo ponto do modelo tem uma vizinhança homeomorfa a um disco (após a identificação dos lados). |
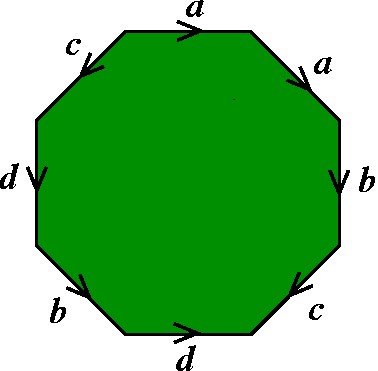
Tomemos, para ilustrar as idéias, o modelo poligonal de 8 lados aabcd-1b-1d-1c-1, mostrado na figura abaixo. |

|
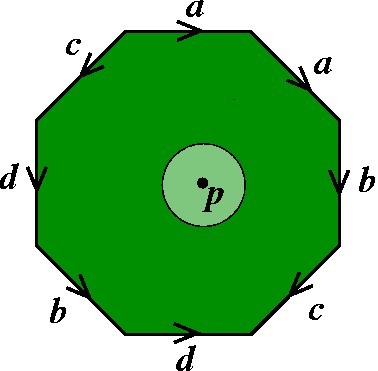
Vejamos as possibilidades. Se um ponto p está fora do contorno do polígono, é fácil achar um disco que rodeia p. |
|
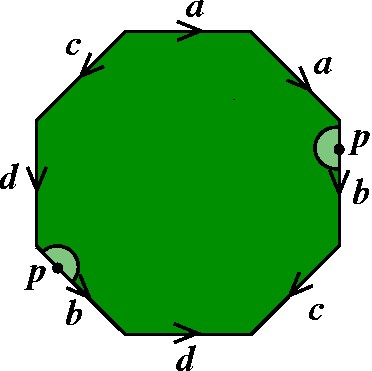
Se o ponto p está sobre o contorno, mas fora de qualquer vértice, também é fácil achar sua vizinhança. |
|
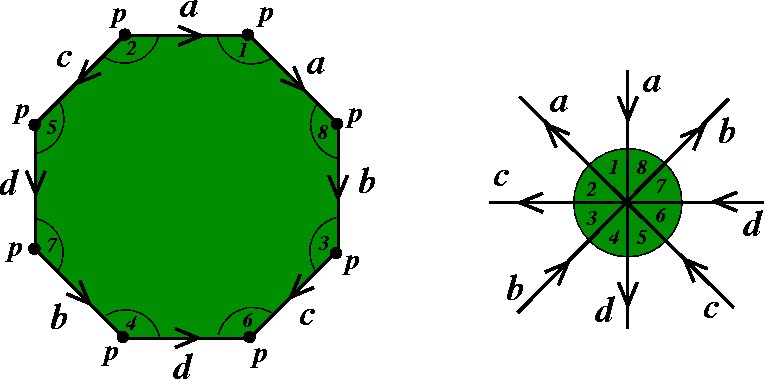
Vejamos agora o caso mais delicado dos pontos sobre os vértices. |
|
Neste exemplo, todos os vértices do polígono representam o mesmo ponto após a identificação, e além disso esse ponto tem uma vizinhança isotópica a um disco. Portanto o modelo poligonal apresentado define uma superfície. |
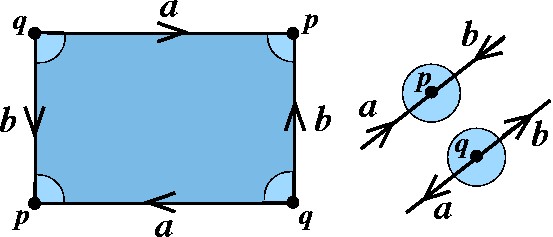
Vejamos agora um caso onde há mais do que um ponto da superfície nos vértices do modelo poligonal. Por exemplo, o modelo retangular do Plano Projetivo tem dois pontos diferentes nos vértices. |
|
Introduziremos uma nomenclatura, neste momento. Diremos que dois vértices do modelo poligonal são equivalentes se representam o mesmo ponto da superfície após a identificação. No modelo retangular do Plano Projetivo, por exemplo, vértices diagonalmente opostos são equivalentes. No modelo anterior, todos os vértices são equivalentes entre si. |
Se v é um vértice, chamamos de classe de equivalência de v ao conjunto de vértices que são equivalentes a v. Se dois vértices são equivalentes é claro que suas classes de equivalência serão iguais. |
Por exemplo, no modelo do Plano Projetivo que apresentamos acima temos duas classes de equivalência, e no modelo anterior apenas uma. |
O número de classes de equivalência de vértices será chamado de ordem nos vértices. |
No entanto não respondemos ainda se todo modelo poligonal pareado define uma superfície. Na verdade, pelo que vimos, o único problema que pode ocorrer é com os pontos de vértice. Mesmo assim, veremos que a resposta é afirmativa! |
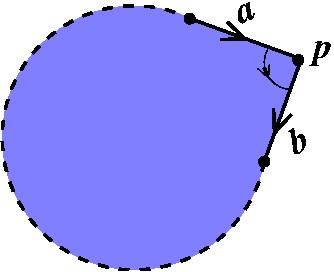
Para ver a razão, considere um modelo poligonal qualquer e escolha um dos vértices, digamos p. Há dois segmentos adjacentes a p, aos quais damos os nomes de a e b (poderia ser um outro lado com a letra a, deixamos ao leitor para pensar nessa possibilidade!). |
|
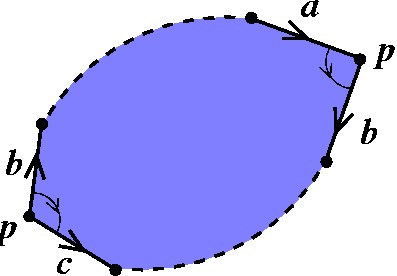
Para continuar, devemos passar para o "outro lado" de b, usando a outra aresta com essa letra. Aí encontramos outro segmento, que indicamos por c. |
|
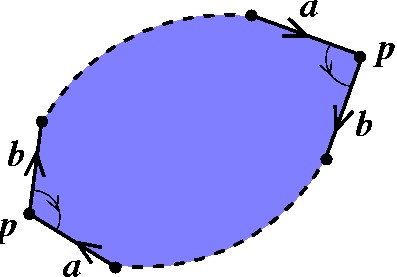
Observe que em vez de encontrar outro segmento c, poderíamos ter encontrado a desta forma: |
|
Nesse caso, seria completada uma volta inteira em torno de p. Note também que, se ao invés disso o segmento com letra a aparecesse invertido então o ciclo não se fecharia: |
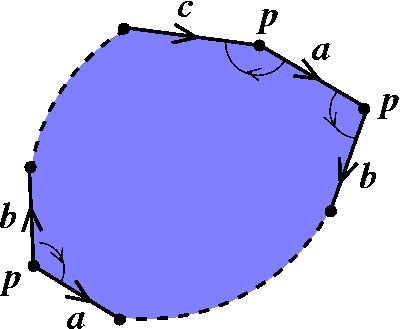
|
No entanto, como não há infinitos lados, em algum momento o ciclo deve se fechar, dando uma volta completa em torno de p. |
A colagem das regiões sombreadas define então a vizinhança de p, isotópica a um disco. |
|
CapXIV-pg10 |
|