CapXIV-pg10
CapXIV-pg11
CapXIV-pg12

 

 

Equivalência entre modelos

 

Agora estamos mais ou menos encaminhados para a demonstração do Teorema de Classificação. Façamos um apanhado de nossas observações.

  • Toda superfície, com ou sem bordo, admite um modelo poligonal, construído por exemplo a partir de uma triangulação.
  • As superfícies com n componentes de bordo (n maior ou igual a 1) admitem modelos poligonais com n buracos. Além disso, quando tampados os buracos esses modelos poligonais são de superfícies sem bordo. Conclusão: uma superfície com n componentes de bordo é homeomorfa a uma superfície sem bordo de onde são retiradas n tampas.
  • Os modelos poligonais de superfícies sem bordo são polígonos com um número par de lados e onde cada letra ocorre aos pares. Denominamos esse tipo de modelo poligonal pareado.

 

Por outro lado, queremos mostrar que toda superfície sem bordo é homeomorfa a uma das superfícies da lista do Teorema de Classificação. Essa lista é formada por:

  • a esfera;
  • somas conexas de n toros, para n maior ou igual a 1;
  • somas conexas de n planos projetivos, para n maior ou igual a 1.

 

Seus modelos são:
esfera:
a a-1
somas conexas de n toros:
a1 b1 a1-1 b1-1 a2 b2 a2-1 b2-1 .... an bn an-1 bn-1
somas conexas de n planos projetivos:
a1 a1 a2 a2 .... an an

 

Bastaria mostrar, portanto, que todo modelo poligonal pareado é homeomorfo a algum desses modelos.

 

Isso deve ser feito a partir de uma série de operações que descreveremos a partir de agora.

 

Começaremos por dois processos simples de simplificação dos modelos.

 

(A) Anulação de letras adjacentes em sentidos opostos.

 

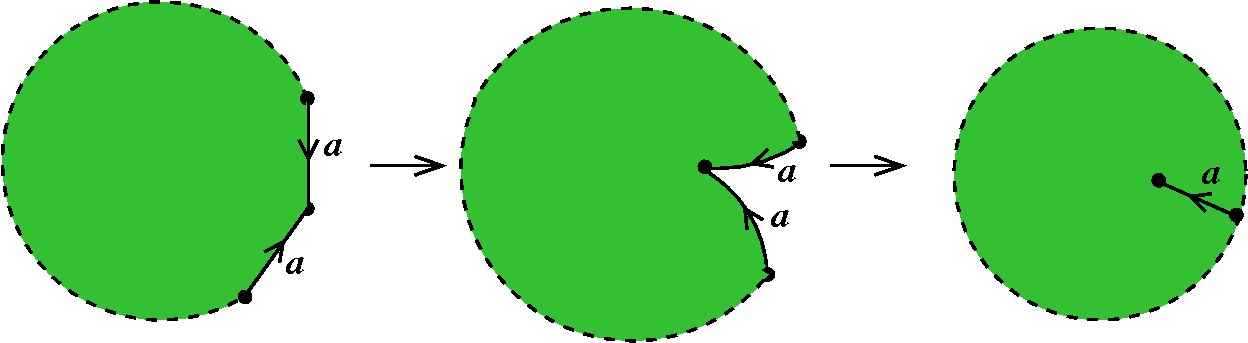
Toda vez que uma letra ocorre em lados adjacentes e com orientações opostas ela pode ser cancelada do modelo poligonal, como já fizemos anteriormente:

 

 

Ou seja, todo bloco do tipo aa-1 pode ser suprimido, a não ser que não haja outras arestas no polígono (no caso da Esfera).

 

(B) Reunião de letras adjacentes numa só.

 

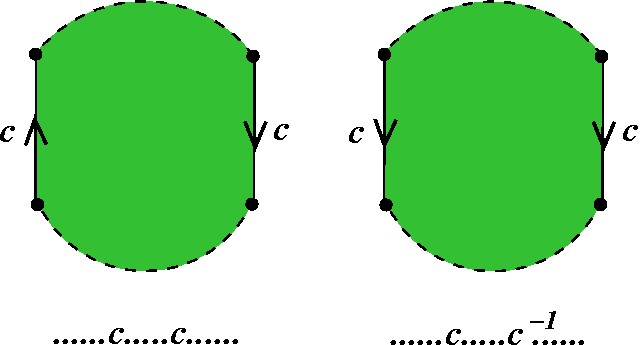
Pode ocorrer no modelo poligonal algo como um destes casos:

 

 

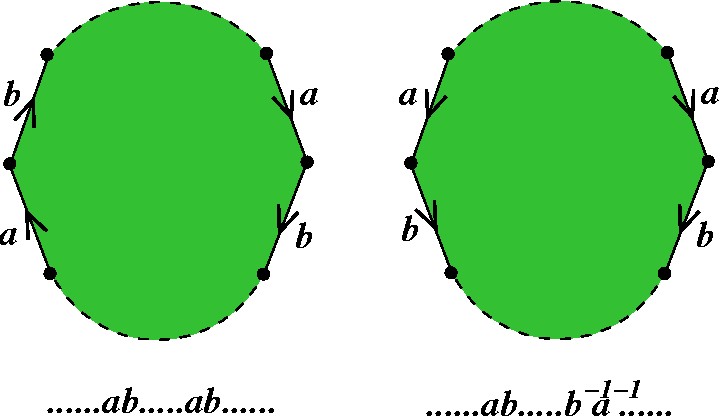
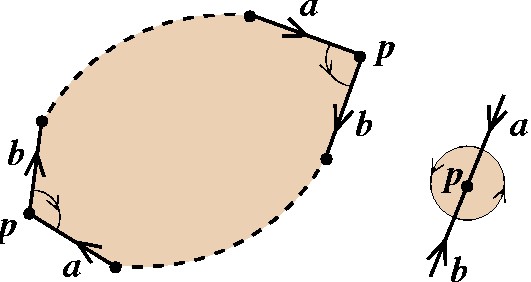
Nestes casos, podemos juntar os segmentos a e b em um só segmento c:

 

 

Lembremos que o artifício já havia sido usado com o Plano Projetivo:

 

 

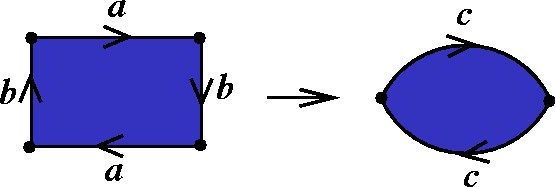
Lembremos que o que vale aqui é o sentido relativo das letras e como elas aparecem. Por exemplo, pode aparecer ....ab-1....ba-1...., mas se invertermos simultaneamente as duas arestas com a letra b ficaremos com ....ab....b-1a-1...., que é um dos casos mostrados. Esta é uma boa maneira de não se confundir, como ilustra este outro exemplo: nada podemos fazer com ....ab-1....b-1a....: se invertermos b, obteremos ....ab....ba...., e isso não permite juntar os dois segmentos num só! É preciso cuidado!!!

 

Uma observação importante é que quando dois vértices podem ser juntados num só então a ordem nos vértices do polígono é maior do que um, pois os dois vértices entre a e b formam uma classe de equivalência, porém há outros vértices que formarão uma ou mais classes de equivalência:

 

 

Logo, ao fazermos a substituição pela letra c reduzimos em uma unidade a ordem nos vértices do polígono.

 

Na verdade, a próxima operação é uma maneira mais geral de reduzir a ordem nos vértices (e inclui essa feita acima). Repetindo essas operações várias vezes, em algum momento ficaremos com uma só classe de equivalência nos vértices do polígono.

 

 
CapXIV-pg10
CapXIV-pg11
CapXIV-pg12