|
|
CapXIV-pg12 |
|
(C) Redução da ordem nos vértices. |
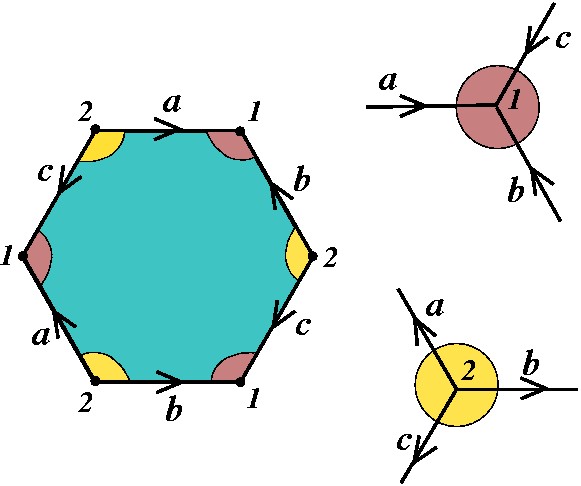
Trabalharemos com um exemplo e veremos que o método deve funcionar em todas as situações. O exemplo tem ordem 2 nos vértices: |
|
|
Nosso objetivo é que só reste o ponto 1 nos vértices. Para isso, vamos recortar e colar o modelo seguidamente, de modo a "completar" a vizinhança de 2. Acompanhe na seqüência abaixo o processo inteiro. |
|
Primeiro, recortamos ao longo de uma linha que liga os dois vértices adjacentes a um dos vértices da classe de equivalência que gostaríamos de eliminar. Com isso, criamos uma nova aresta, que chamamos de d. |
|
|
O triângulo recortado é colado de volta ao modelo por uma das arestas já existentes. Na figura, colamos pela letra c, mas poderíamos fazê-lo também pela letra a, só que para tanto teríamos que fazer uma reflexão no triângulo. |
|
|
Mais um recorte é feito, ao longo da linha que une os vértices adjacentes ao vértice 2 isolado. Esse pedaço é colado do outro lado do modelo, completando a vizinhança do vértice 2 e fazendo com que esse ponto passe a estar no interior do modelo, e não mais em seu contorno. Neste exemplo, o modelo resultante é facilmente identificável como sendo o de um Toro. |
|
Observe que em nenhum momento do processo aparece um novo ponto sobre os vértices que não seja um já existente. Assim, reduz-se em uma unidade a ordem nos vértices. Aplicando-se o procedimento tantas vezes quantas forem necessárias, concluímos que: todo modelo poligonal pareado é equivalente a um outro modelo poligonal pareado de ordem 1 nos vértices. |
Observe também que as técnicas descritas em (A) e em (B) estão incluídas na técnica (C) que acabamos de descrever. |
Portanto para demonstrar o Teorema de Classificação nos basta apenas mostrar que todo modelo poligonal pareado de ordem 1 nos vértices é equivalente a um dos modelos a a-1 (Esfera), a1 a1 a2 a2 .... an an (soma conexa de n Planos Projetivos) ou a1 b1 a1-1 b1-1 a2 b2 a2-1 b2-1 .... an bn an-1 bn-1 (soma conexa de n Toros). |
Não podemos nos esquecer de prestar atenção para que o trabalho feito até o momento não seja desmanchado. Para ser específico, cada operação que fizermos a partir de agora não poderá aumentar a ordem nos vértices. |
De fato, isso não irá ocorrer. |
|
CapXIV-pg12 |
|