|
|
CapXIV-pg13 |
|
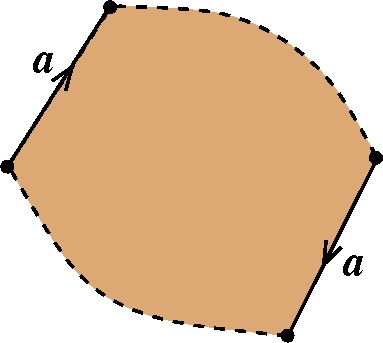
Um de nossos objetivos � que pares de segmentos que tenham o mesmo sentido, isto �..... |

|
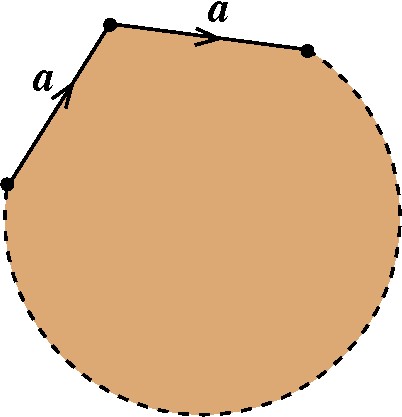
...s� apare�am no modelo um ao lado do outro, desta maneira: |
|
Para facilitar a exposi��o, chamaremos de pares desorientadores aos pares de segmentos que t�m a mesma orienta��o no pol�gono. Aos demais pares de segmentos chamaremos de pares neutros. A raz�o dos nomes � clara: lembre-se do que acontece com as antenas de Aderbal quando ele atravessa um par desorientador! |
(D) Pares desorientadores ficam adjacentes. |
Tome um modelo poligonal com um par desorientador n�o adjacente: |

|
Cortamos o modelo por um segmento b como abaixo e colamos em a: |

|
Agora temos um modelo poligonal onde um par desorientador n�o adjacente foi substitu�do por um adjacente. Aten��o: n�o est� certo pensar que o m�todo junta o par desorientador n�o adjacente. O que acontece � que o par desorientador n�o adjacente desaparece no interior do modelo e outro par desorientador aparece no lugar dele, s� que o novo par � adjacente. |
Pode-se ent�o perguntar: e se j� houvesse um par desorientador adjacente, ele poderia ser separado por essa opera��o? A resposta a esta pergunta � crucial para saber se podemos um a um ir substituindo pares n�o adjacentes por pares adjacentes, at� que todos os pares desorientadores fiquem adjacentes! |
A resposta � que pares adjacentes n�o se separam! A figura abaixo d� uma id�ia do porqu� (e nem importam as orienta��es dos segmentos). |

|
Tamb�m a ordem nos v�rtices n�o aumenta, e o n�mero de lados do modelo permanece o mesmo. |
Ent�o podemos repeti-lo um certo n�mero de vezes at� que todos os pares desorientadores estejam adjacentes! |
|
CapXIV-pg13 |
|