
|
|
CapXIV-pg14 |
|
(E) Pares neutros. |
Nos modelos de somas conexas de Toros, pares neutros aparecem dispostos da seguinte maneira: |

|
Deveria ser possível então agrupar todos os pares neutros dessa forma. O procedimento é assim descrito. |
(1) Escolha um par neutro, se houver (se não houver nenhum, não há mais nada a fazer!). |

|
Esse par neutro não deve ser adjacente. Se fosse, ele já teria sido eliminado pelo método (A). |
(2) Agora devemos descobrir um outro par neutro que se alterne com esse, do seguinte modo: |
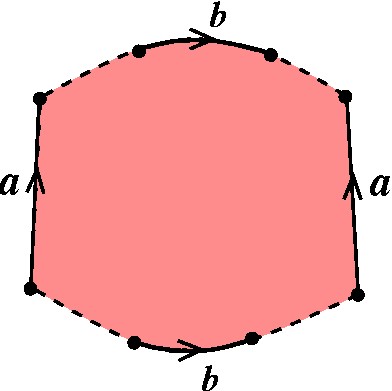
|
Na verdade, temos que provar que existe pelo menos um par neutro dessa forma, lembrando que no atual estágio nosso modelo já deve ter passado por todas as etapas anteriores: passando por (A), (B) e (C), sua ordem nos vértices deve ser igual a 1 e passando por (D), todos os seus pares desorientadores são adjacentes. |
Suponhamos que não haja, isto é, ou não há nenhum outro par neutro, ou então qualquer outro par neutro está numa das seguintes posições, não alternadas com a letra a: |
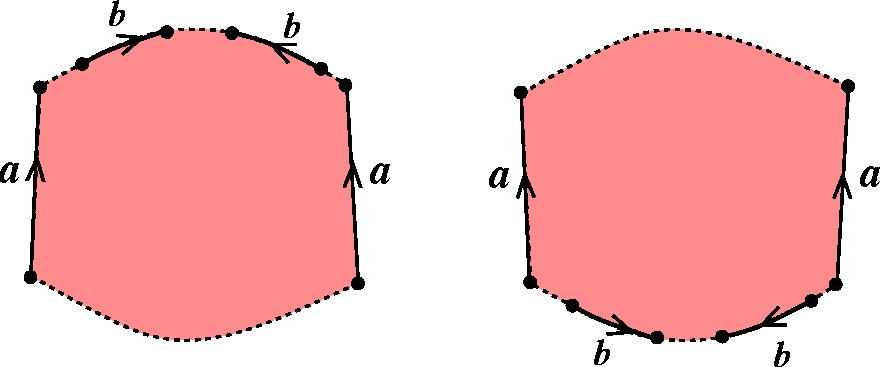
|
Mostraremos que essa suposição leva a uma contradição com o fato de que a ordem nos vértices é igual a 1. |
Nossa suposição implicaria que todos os pares além da letra a ou estariam do lado de "cima" ou do lado de "baixo", isto é, nenhum par alternaria com a. Isso porque todos os pares desorientadores já estão adjacentes, e nós estamos exatamente supondo que não há pares neutros alternando com a. Chegamos então à conclusão que os vértices de "cima" só se identificariam com os vértices de "cima", e os vértices de "baixo" só se identificariam com os vértices de "baixo". Haveria portanto pelo menos duas classes de equivalência de vértices, uma totalmente em "cima" e outra totalmente em "baixo", que contradiz o fato de que a ordem nos vértices é igual a 1. |
Veja um exemplo com 3 classes de equivalências. Nesse caso, duas em "cima" (1 e 2) e uma em "baixo" (3). |
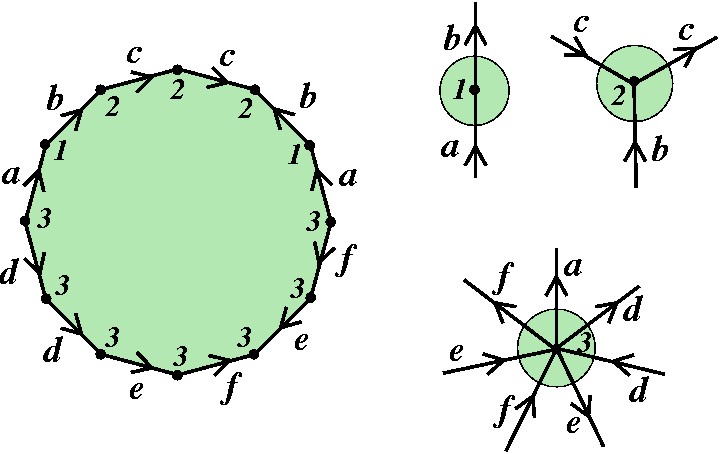
|
Logo nossa suposição estava errada, e obrigatoriamente temos a situação esperada: |

|
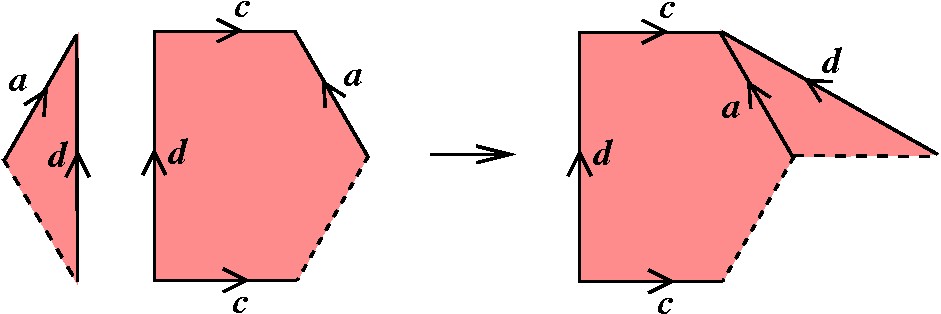
(3) Finalmente realizamos o agrupamento desses segmentos, ou melhor, a substituição desses segmentos por dois pares neutros em posição adjacente e alternada, como desejado inicialmente. Para isso, cortamos ao longo do segmento c, que une duas pontas de a, e colamos os lados com a letra b. |
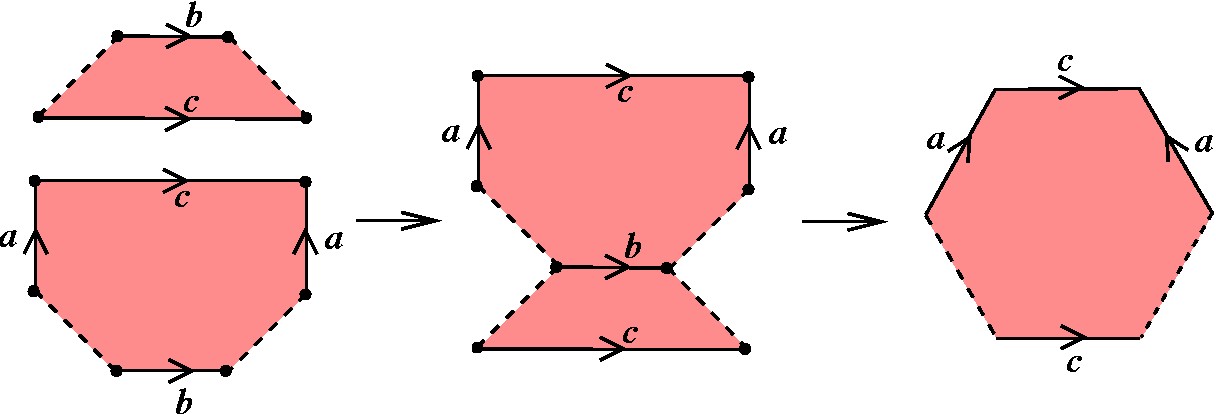
|
Cortamos de novo, desta vez ao longo de d (que une extremos de c) e colamos em a. |
|
Note que o polígono ficou igual a ....c-1dcd-1..... Invertendo as duas arestas com a letra c, isso é equivalente a ter ...cdc-1d-1...., que é a forma desejada desde o início. |
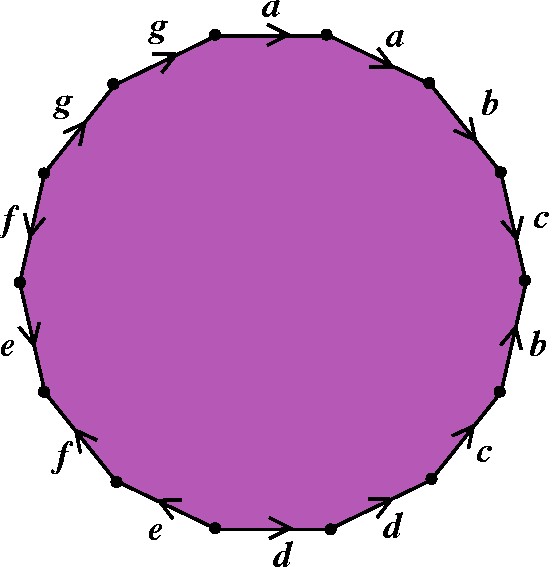
Note que mais uma vez nada do que foi feito anteriormente é anulado. E, além disso, se tiverem restado outros pares neutros para agrupar, repetimos o procedimento tantas vezes quantas forem necessárias. Chegaremos a um modelo que tem todos os pares desorientadores adjacentes e todos os pares neutros agrupados, de dois em dois, da forma proposta. O modelo poligonal da figura abaixo é um exemplo: |
|
Nesse exemplo (aabcb-1c-1d-1d-1efe-1f-1gg) a superfície resultante é claramente a soma conexa de dois Toros com três Planos Projetivos. |
|
CapXIV-pg14 |
|