|
|
CapXIV-pg15 |
|
Já podemos considerar demonstrado o Teorema de Classificação, pois as simplificações e operações (A), (B), (C), (D) e (E) mostram que a superfície é homeomorfa à soma conexa de um certo número n de toros com um certo número m de planos projetivos. |
Porém pelo exposto no Capítulo XII, ela é homeomorfa à soma conexa de 2n + m planos projetivos, se m for maior ou igual a 1. Se m = 0 então ela é uma superfície orientável, soma conexa de n toros. Ou é simplesmente uma esfera (n=0, m=0). |
O que faremos agora é mostrar que uma parte dos argumentos do Capítulo XII pode ser dispensada, e mostrar diretamente que a soma conexa de n toros com m planos projetivos (para m maior ou igual a 1) é a soma conexa de 2n+m planos projetivos. |
Em outras palavras, iremos mostrar que se um modelo poligonal está na forma final, como no exemplo ao fim da página anterior, e tem pelo menos um par desorientador, então todos os pares neutros podem ser substituídos por pares desorientadores. Ou seja, todos os "Toros" são substituídos por dois "Planos Projetivos". Tudo isso é feito por manipulação do modelo, como vimos fazendo até agora. |
(F) Substituição de pares neutros por pares desorientadores em superfícies não-orientáveis. |
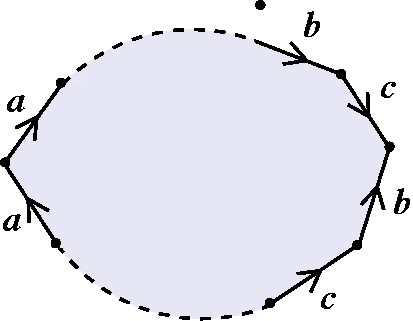
Observe primeiro que, como a superfície é não-orientável, existe pelo menos um par desorientador. Então escolha no modelo um par desorientador e dois pares neutros alternados, como abaixo: |

|
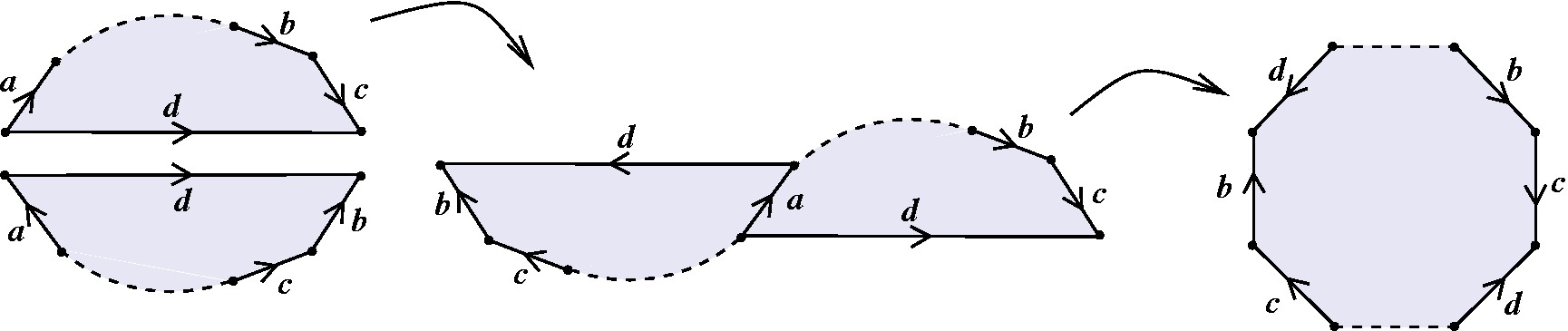
Corte pelo segmento d, como mostrado no desenho abaixo, e cole em a: |
|
Ficam três pares desorientadores, mas não adjacentes, em vez de um par desorientador e dois pares neutros. Agora pode-se implementar o processo descrito em (D) para substituir esses pares desorientadores por pares desorientadores adjacentes. |
E aqui termina a prova do Teorema de Classificação! |
|
CapXIV-pg15 |
|