|
|
CapXIII-pg4 |
|
Para fazer uso prático do Teorema de Classificação, tomemos como exemplo as superfícies A e C de (....). |
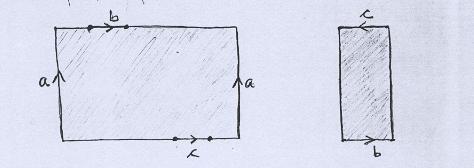
Superfície A Não é difícil ver que ela pode ser definida via identificação como mostrado abaixo. |

|
Calculamos sua característica de Euler em (...): X = -1. |
Como a superfície é não-orientável e tem uma só componente de bordo, pelo Teorema de Classificação ela deve ser a Garrafa de Klein menos uma tampa. |
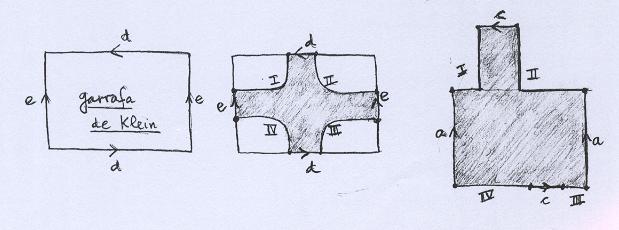
De fato, a Superfície A corresponde à área sombreada na Garrafa de Klein desenhada abaixo (os segmentos de bordo numerados indicam a correspondência). |
|
As partes restantes formam a tampa retirada. |
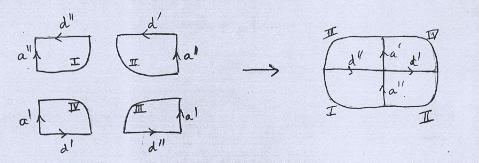
|
Superfície C Ela fica assim definida, via identificação. |
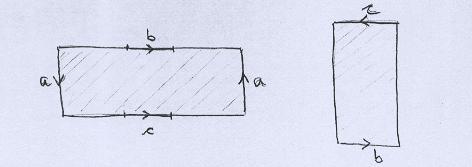
|
Calculamos sua característica de Euler, usando o seguinte grafo. |
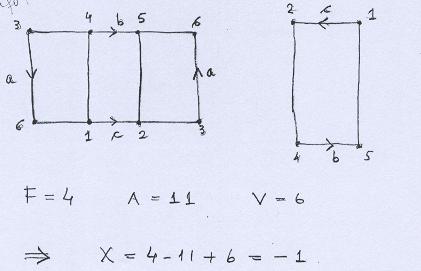
|
Como a Superfície C tem característica de Euler igual a -1, é não-orientável e tem duas componentes de bordo, usando o Teorema de Classificação deduzimos que ela é homeomorfa ao Plano Projetivo sem duas tampas. Como no caso anterior, ela corresponde à área sombreada do desenho abaixo. |
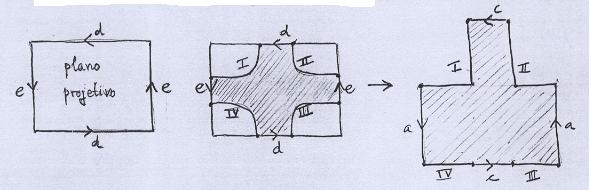
|
Só que agora as partes restantes formam dois discos, exatamente as duas tampas retiradas. |
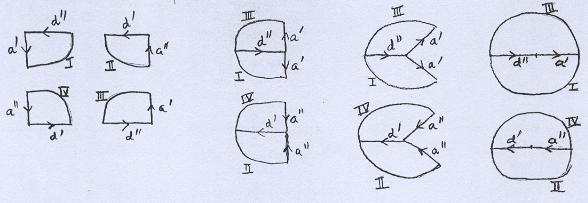
|
Agora olhemos para um exemplo mais complicado, na figura abaixo: uma superfície não-orientável cuja única componente de bordo é um nó. Antes de tudo, tente ver por que ela não é orientável! |
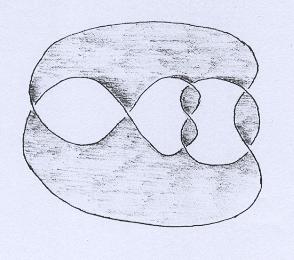
|
Primeiro definimos a superfície via identificação de pedaços do plano e calculamos sua característica de Euler. |
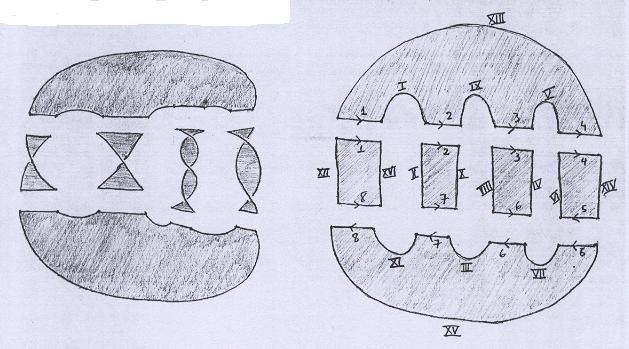
|
Vemos 6 faces, 24 arestas (16 segmentos de bordo, em algarismos romanos e 8 segmentos de identificação conectando as faces, em algarismos arábicos) e 16 vértices. A característica de Euler vale então -2. |
Como a superfície tem uma só componente de bordo (pois o bordo é um nó, não um enlace) e não-orientável, ela corresponde a uma superfície não-orientável de característica de Euler igual a -1 sem uma tampa. Usando o diagrama de classificação, concluímos que essa superfície é a soma conexa do Toro com o Plano Projetivo sem uma tampa. |
Se o leitor quiser ver isso diretamente, o desenho abaixo indica como deve ser feito o homeomorfismo. |
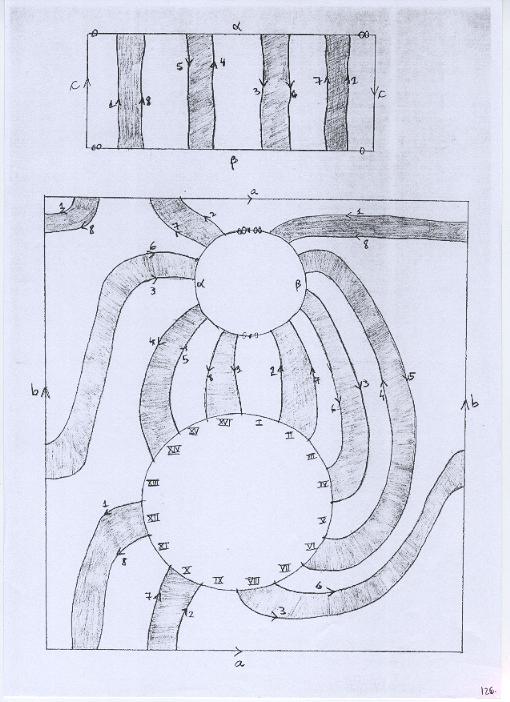
|
Complicado, não? Ainda bem que tínhamos o Teorema para saber por onde começar....! |
|
CapXIII-pg4 |
|