|
|
CapXIII-pg3 |
|
Superfícies não-orientáveis |
O enunciado do Teorema é semelhante neste caso, mas aqui o papel do toro é desempenhado pelo Plano Projetivo. |
Teorema de Classificação para superfícies orientáveis sem bordo. Toda superfície não-orientável sem bordo é homeomorficamente equivalente à soma conexa sucessiva de m Planos Projetivos, para algum número natural m maior ou igual a 1. |
O número m é o gênero da superfície não-orientável. |
Já vimos que a soma conexa de um Plano Projetivo a uma superfície qualquer diminui em uma unidade sua característica de Euler. Como o Plano Projetivo tem característica de Euler igual a 1, a soma conexa de m Planos Projetivos tem característica de Euler igual a 2-m (ou, invertendo a fórmula, m=2-X. |
A Garrafa de Klein, por exemplo, é a soma conexa de dois Planos Projetivos, e tem característica de Euler zero. |
Se somarmos um toro a uma superfície não-orientável, isso será equivalente a somar dois Planos Projetivos, como vimos no Capítulo XII. Neste caso, a soma conexa de um toro diminui em duas unidades o gênero da superfície (enquanto que só diminui o gênero em uma unidade, se a superfície é orientável). |
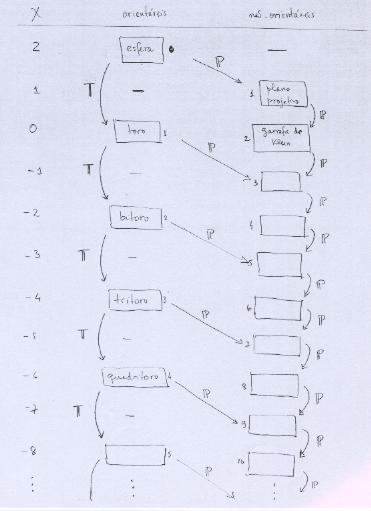
Juntando os dois enunciados, relativos às superfícies sem bordo orientáveis e não orientáveis, podemos representar por um diagrama o conjunto de todas elas. |

|
No diagrama, a coluna da esquerda indica a característica de Euler. Depois listamos em duas colunas separadas as superfícies orientáveis e não-orientáveis. Um traço simples indica que não existe uma superfície com a orientabilidade e a característica de Euler especificada. Um retângulo indica que tal superfície existe, e seu nome usual está inscrito dentro (muitas das superfícies, no entanto, não recebem um nome específico). |
As flechas indicam a hierarquia das somas conexas: T é o toro e P é o Plano Projetivo. Por exemplo, a superfície que é a soma conexa do Bitoro com o Plano Projetivo é não-orientável e tem característica de Euler igual a -3. Ela é equivalente à soma conexa de 5 Planos Projetivos. |
Finalmente, o número ao lado dos retângulos indica o gênero da superfície. A numeração do gênero é independente na coluna das superfícies orientáveis e na coluna das superfícies não-orientáveis. |
Para exercitar o uso do diagrama, tentemos responder à seguinte pergunta: "Quantas superfícies existem, com ou sem bordo, com característica de Euler igual a zero?" Evidentemente aqui está implícito que não contaremos repetidamente superfícies que são homeomorfas entre si. |
Bom, sem bordo são duas: o Toro (orientável) e a Garrafa de Klein (não-orientável). Agora suponha que S0 é uma superfície com n componentes de bordo e que X(S0)=0. Identificando as componentes de bordo com bordos de discos, "tapamos" os buracos das superfícies, formando uma nova superfície S sem bordo. Além disso, a característica de Euler da nova superfície S é a característica de Euler da antiga S0, que supusemos igual a zero, mais n, por causa do número de tampas acrescidas. |
Então é só examinar caso a caso. Se S0 tem uma componente de bordo (n=1), então S tem característica de Euler igual a 1. Portanto, pelo diagrama, S só pode ser o Plano Projetivo, e S0 tem que ser o Plano Projetivo sem uma tampa, isto é, a Faixa de Moebius. |
No caso de S0 ter duas componentes de bordo (n=2), teremos X(S)=2, e portanto S é uma esfera. Concluímos que S0 é uma esfera sem duas tampas, ou seja, o cilindro. |
Agora, se S0 tivesse três ou mais componentes de bordo (n > 2), teríamos X(S) > 2. Mas não existe superfície com característica de Euler maior do que 2, o que nos levaria a uma contradição. Em outras palavras, não existe superfície com três ou mais componentes de bordo e característica de Euler igual a zero! |
Ao final, encontramos quatro superfícies: o Toro, a Garrafa de Klein, a Faixa de Moebius e o Cilindro. |
|
CapXIII-pg3 |
|