|
|
CapXIII-pg2 |
|
Dentre as superfícies sem bordo, distinguimos dois tipos: as orientáveis e as não-orientáveis. Enunciaremos o Teorema de Classificação separadamente nos dois casos. |
Superfícies orientáveis |
A Esfera, o Toro e o Bitoro foram exemplos dados. O Bitoro, como vimos no Capítulo XII, é a soma conexa de dois toros. Na verdade, pensando de um modo geral, se S0 é uma superfície orientável, sua soma conexa com o Toro também é orientável. Isso nos dá uma maneira de construir novas superfícies orientáveis pela soma conexa sucessiva de toros às supefícies já existentes. Assim geramos tritoros, quadritoros, etc. O Teorema de Classificação nos diz que essa é a única maneira de se produzir superfícies orientáveis sem bordo. |
Teorema de Classificação para superfícies orientáveis sem bordo. Toda superfície orientável sem bordo é homeomorficamente equivalente a uma esfera ou à soma conexa sucessiva de n toros, para algum número natural n. |
Antes de discutirmos a classificação das superfícies não-orientáveis, vejamos como fazer uso desse Teorema. |
Como vimos no Capítulo XII, cada toro que somamos diminui em duas unidades a característica de Euler. A Esfera tem característica de Euler X igual a 2, o toro tem X=0, o bitoro tem X=-2, etc. A soma conexa de n toros tem X = 2 - 2n . |
Na verdade já discutimos esse assunto no Capítulo VII, mas lá em vez de somar toros falávamos em adição de alças. O número n é chamado de gênero da superfície. Convenciona-se que a Esfera tenha gênero zero. |
Se nos é dada uma superfície qualquer, orientável e sem bordo, sabemos pelo Teorema que ela é homeomorficamente equivalente a uma esfera ou à soma conexa de n toros, para algum n maior ou igual a 1. Como saber quanto vale n? |
Ora, basta calcular a característica de Euler da superfície. Se for igual a -8, por exemplo, significa que n = 5, pois -8 = 2 - 2 · 5 . |
O Teorema também nos informa que não existem superfícies orientáveis, sem bordo, com característica de Euler maior do que 2! E também que não existem superfícies desse tipo com característica de Euler igual a 1, -1, -3, -5, etc. Os únicos valores possíveis para a característica de Euler de superfícies orientáveis sem bordo são o 2 (esfera), o zero (toro), o -2 (bitoro), o -4 (tritoro), o -6 (quadritoro), etc. |
De forma geral, podemos obter o gênero a partir da característica de Euler através da equação n = 1 - X/2 , que é a equação X = 2 - 2n resolvida para n. |
Para ilustrar um pouco mais, vejamos um exemplo em que o Teorema de Classificação é bastante útil. |
Consideremos a superfície de Seifert do nó trifólio construída no Capítulo XI (de fato, obtivemos dois modelos diferentes, mas para os dois será igualmente válido o raciocínio). Chamemos de S0 essa superfície, que é orientável e tem uma componente de bordo. Colando um disco ao bordo teremos uma superfície orientável e sem bordo, a qual chamaremos de S. |
No Capítulo VII vimos que a adição de tampas aumenta em uma unidade a característica de Euler. Portanto X(S) = X(S0) + 1 Para calcular X(S0) temos que ver como S0 foi construída. |
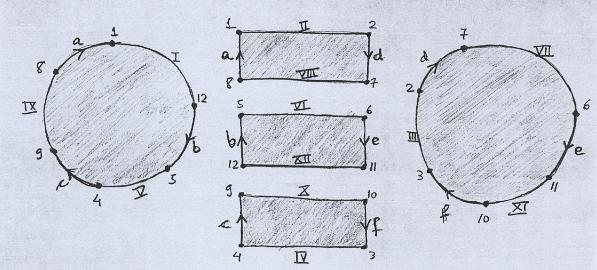
Não é difícil ver que ela é homeomorfa à seguinte superfície, definida via identificação. Os discos correspondem às regiões maiores da montagem e os retângulos às tiras que as ligam. |

|
Na figura temos:
|
Como há 5 faces, então a característica de Euler da superfície S0 é 5 - 18 + 12, isto é, -1. Em conseqüência, a característica de Euler da superfície S, que é S0 acrescida de uma tampa, é zero. |
Então S é uma superfície orientável sem bordo com característica de Euler igual a zero. Pelo Teorema de Classificação, essa superfície é homeomorfa a um toro, e por conseguinte a superfície original S0 é um toro sem uma tampa! |
Tudo bem, desde que acreditemos no Teorema! Mas... será que não tem um jeito direto de ver que essas superfícies de Seifert do nó trifólio são homeomorfas a um toro sem uma tampa? |
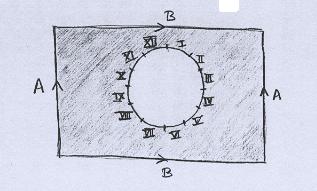
Bom, tentemos..... No desenho abaixo temos um toro sem uma tampa. O bordo da tampa é dividido em 12 segmentos, que numeramos com algarismos romanos. |
|
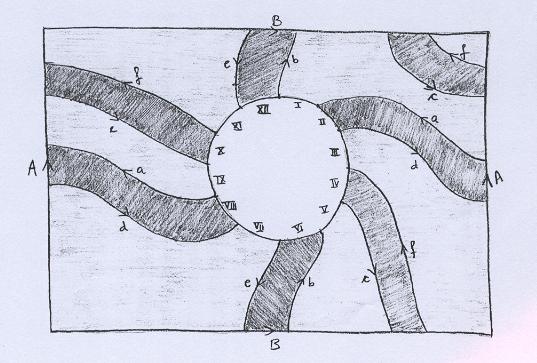
Nosso objetivo é recortar essa figura em 5 pedaços: três tiras e dois discos, cujas orientações de identificação sejam exatamente iguais àquelas da superfície de Seifert do nó trifólio. O recorte é feito baseado na figura seguinte. |
|
As áreas sombreadas em tom mais forte correspondem às três tiras. O primeiro passo então é recortar a figura e compor essas três tiras. |
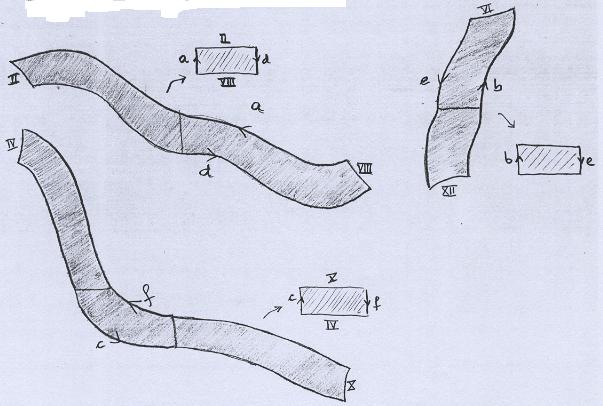
|
Ficam para serem arranjados os pedaços restantes: |
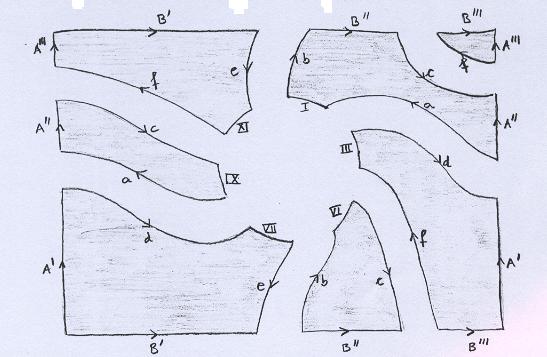
|
Colando segundo A', A'', A''' e B', B'', B''', obtemos os dois discos restantes: |
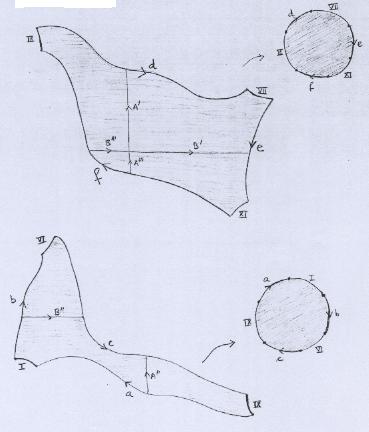
|
Ufa! Funcionou! De qualquer forma, tivemos que contar com o Teorema para saber por onde começar! |
Para quem achou isso muito complicado, um consolo: no próximo Capítulo teremos formas menos intrincadas de descobrir com que superfície estamos lidando! |
|
CapXIII-pg2 |
|