|
|
CapXII-pg6 |
|
Para terminar este Capítulo, vejamos como a característica de Euler é afetada por somas conexas. Mais precisamente, sejam S1 e S2 duas superfícies e S1#S2 como sendo a soma conexa das duas. Será que podemos escrever a característica de Euler X(S1#S2) da nova superfície S1#S2 em função das características de Euler X(S1) e X(S2) das superfícies originais? |
A resposta é sim e o método é o mesmo do Capítulo VII. Definimos uma triangulação em S1 com F1 faces, A1 arestas e V1 vértices, e uma triangulação em S2 com F2 faces, A2 arestas e V2 vértices. Então X(S1) = F1 - A1 + V1 e X(S2) = F2 - A2 + V2. |
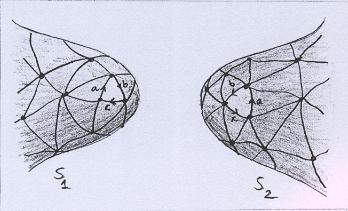
Agora retiramos uma tampa de cada superfície. Aqui escolhemos as tampas como sendo faces das triangulações, como mostra a figura abaixo. Também identificamos os bordos das tampas, fazendo coincidir arestas com arestas e vértices com vértices. |

|
Ao colarmos, temos automaticamente uma triangulação para S1#S2, com F faces, A arestas e V vértices. Só que F é igual à soma de F1 com F2 menos dois, por causa das duas tampas retiradas: F = F1 + F2 - 2 O número de arestas A é A1 + A2 - 3, pois 3 arestas são identificadas e não podem ser contadas duas vezes. Para os vértices é a mesma coisa: V = V1 + V2 - 3. Então
|
Conclusão: vale a fórmula
|
Por exemplo, o Toro tem característica de Euler igual a zero. Então a soma conexa de uma superfície S qualquer com o Toro é uma superfície de característica de Euler igual a X(S) + 0 - 2. Em outras palavras, somar um toro diminui em duas unidades a característica de Euler. Somar uma Garrafa de Klein tem o mesmo efeito, pois sua característica de Euler também é igual a zero. Já o Plano Projetivo tem característica de Euler igual a 1, portanto a superfície resultante tem característica de Euler X(S)+1-2 = X(S) -1. |
|
CapXII-pg6 |
|