|
|
CapXII-pg5 |
|
Observamos que a soma conexa de uma superfície S com o Toro pode não ser equivalente à soma conexa dessa mesma superfície S com a Garrafa de Klein. Exemplificamos esse fato quando S é a esfera. No entanto, vamos mostrar agora o seguinte fato, que é de alguma forma surpreendente: se S é uma superfície não-orientável então a soma conexa de S com um Toro é homeomorfa à soma conexa de S com uma Garrafa de Klein. |
Em outras palavras, se S é não-orientável tanto faz se somamos um Toro ou uma Garrafa de Klein (ou dois Planos Projetivos) a S que o resultado será sempre o mesmo! Pensando em alças, isso é o mesmo que dizer que os modos (i), (ii), (iii) e (iv) são todos equivalentes se S é não-orientável. Mas atenção: isso não é verdade se S for orientável! |
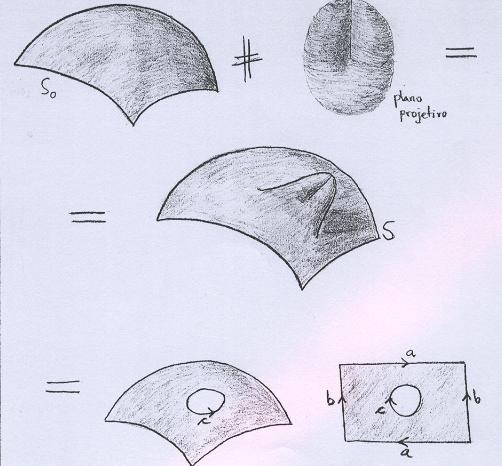
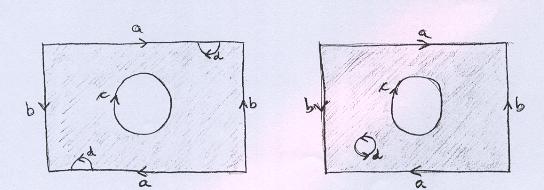
Para simplificar os argumentos, vejamos primeiro o caso em que S é uma superfície obtida a partir da soma conexa de uma superfície qualquer S0 com o Plano Projetivo. Abaixo ilustramos a superfície, na sua representação dentro do espaço ambiente, com auto-interseção, e também uma maneira de defini-la através de colagem: o bordo da tampa retirada de S0 é identificado com o bordo da tampa retirada do Plano Projetivo, e o Plano Projetivo é mostrado como a identificação dos lados de um retângulo, com as orientações indicadas (TEM UM ERRO NO DESENHO, NO PLANO PROJETIVO, UMA DAS LETRAS b TEM QUE SER TROCADA). |

|
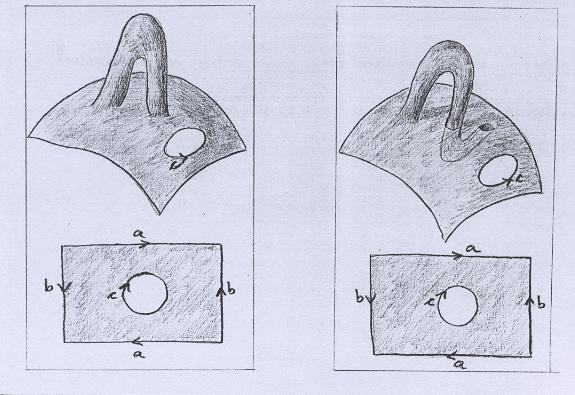
Nosso objetivo é mostrar que as duas superfícies abaixo são equivalentes. |
|
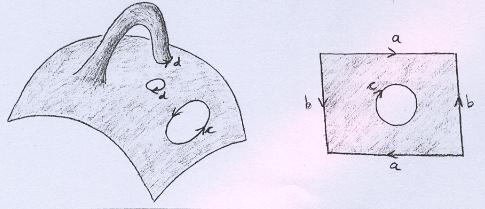
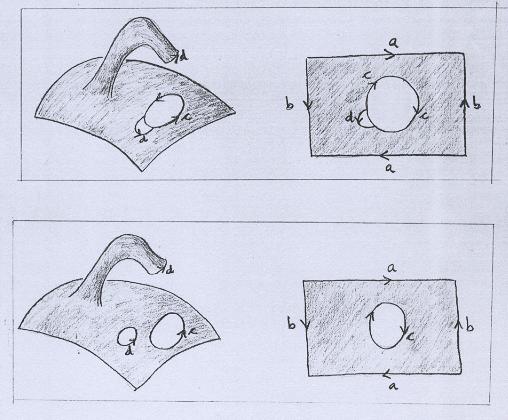
Começamos pela superfície do lado direito. Primeiramente soltamos uma das pontas da alça, para facilitar a visualização, e marcamos a maneira certa de ser refeita a colagem. |
|
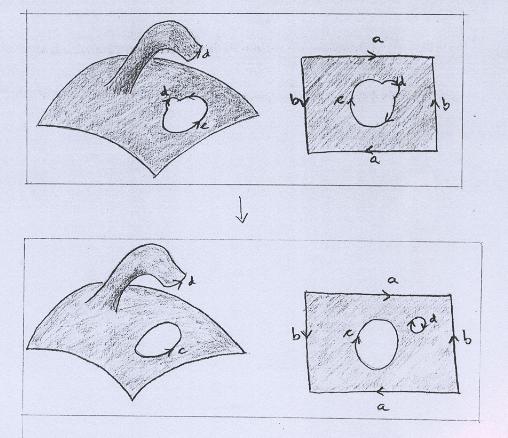
Então deformamos a superfície de tal modo que a curva d se desloque, atravessando a curva c. |
|
Continuamos arrastando a curva d, para que atravesse o segmento a do retângulo. |
|
Justamente porque o Plano Projetivo é não-orientável, foi possível "inverter" a orientação de d. Então fazemos atravessar novamente a curva d por c. |
|
Pronto! Agora é só colar em d! |
Note que o mesmo raciocínio pode ser aplicado para qualquer superfície não-orientável. Nessas superfícies sempre há um caminho a ser percorrido pela curva d (um caminho desorientador) que inverte sua orientação (como as antenas de Aderbal, que trocam de lado). |
|
CapXII-pg5 |
|