|
|
CapXII-pg4 |
|
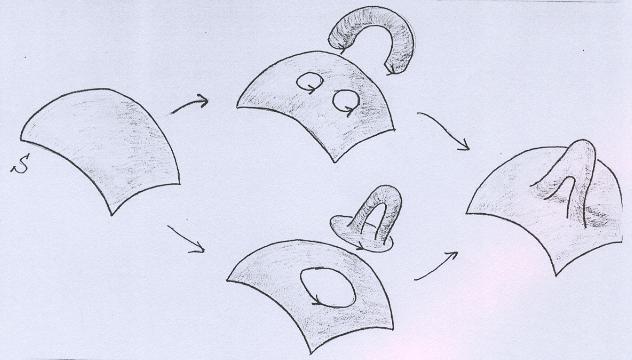
O acréscimo de alças não se encaixa muito bem, a princípio, na definição que demos de soma conexa. Mas isso é só uma questão de ponto de vista. Veja que as duas operações abaixo produzem o mesmo resultado. |

|
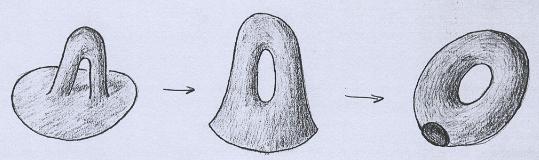
Em vez de tirarmos duas tampas e colarmos um cilindro, tiramos apenas uma tampa e colamos uma superfície que é homeomorfa ao toro sem uma tampa: |
|
Então o que de fato realizamos foi a soma conexa da superfície S com um toro! |
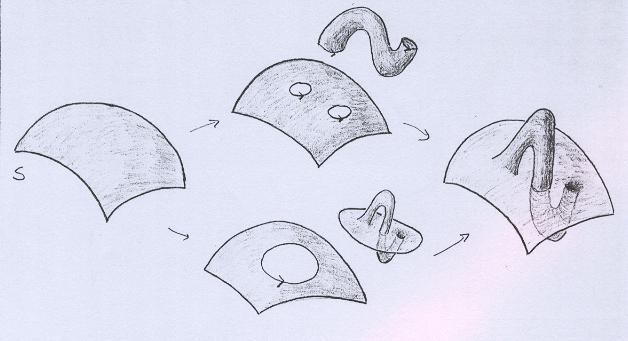
O outro caso é análogo: |
|
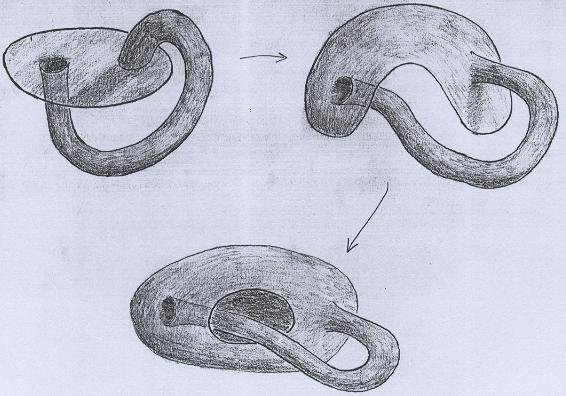
Neste caso, ao invés do toro sem uma tampa, acrescentamos uma Garrafa de Klein sem uma tampa. Para ver porque a superfície adicionada é uma Garrafa de Klein sem uma tampa, acompanhe a seqüência abaixo. |
|
Em resumo, acrescentar uma alça a uma superfície S, que constitui em tirar duas tampas de S e acrescentar um cilindro, é o mesmo que fazer a soma conexa de S com o Toro ou a Garrafa de Klein. |
Por outro lado, a própria Garrafa de Klein é a soma conexa de dois Planos Projetivos. Ou seja, cada par de Planos Projetivos somados equivale a somar uma Garrafa de Klein. |
|
CapXII-pg4 |
|