|
|
CapXII-pg3 |
|
Agora passamos à segunda observação, que também nos será importante mais adiante. |
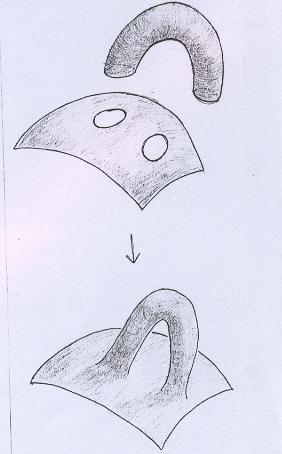
No Capítulo VII vimos que podemos obter novas superfícies a partir do acréscimo de "alças". Na operação (vide figura abaixo), tem-se de início uma superfície S da qual são retiradas duas tampas e então é acrescentado um cilindro por identificação dos bordos. |

|
Não comentamos na ocasião, mas há algo indeterminado nessa definição. |
Lembre-se que no Capítulo IX aprendemos que para indicar as identificações a serem feitas precisamos orientar os segmentos. No exemplo desenhado acima, teríamos algo assim: |
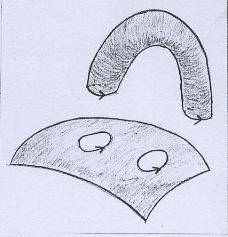
|
No entanto, se invertêssemos a orientação de um dos bordos do cilindro, a colagem deveria ser feita de outro modo. Por exemplo, se a superfície S fosse a esfera, então teríamos: |
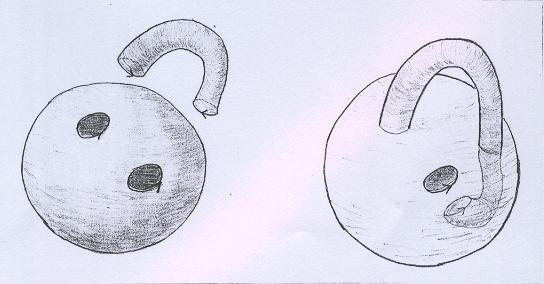
|
Note que fomos obrigados a provocar uma auto-interseção para conseguir colar a alça. No exemplo mostrado, a superfície resultante é a Garrafa de Klein. Isso porque podemos colar primeiro um dos bordos, obtendo em seguida, com deformação, um cilindro com componentes de bordo a serem identificadas. A orientação das componentes de bordo indica que a superfície é a Garrafa de Klein. |
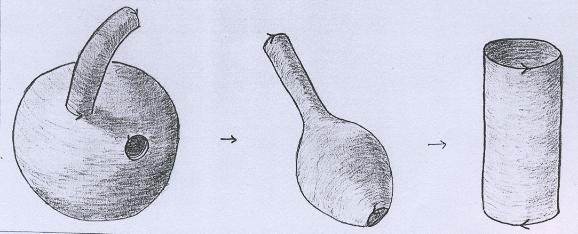
|
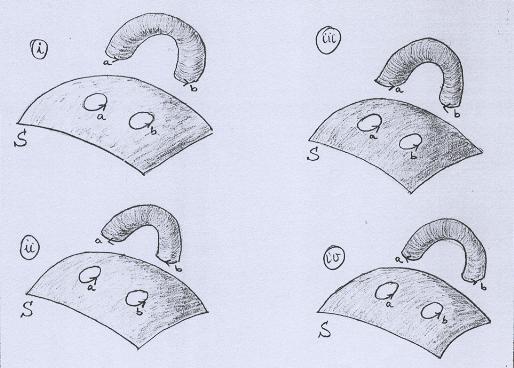
A rigor ainda teríamos mais dois casos a considerar, no que se refere à maneira de colar alças, totalizando quatro, como mostra a figura abaixo. |
|
Obviamente estamos preocupados com as orientações relativas, e por isso fixamos as orientações dos bordos das tampas retiradas de S, deixando variar as orientações das componentes de bordo do cilindro. |
As maneiras (iii) e (iv) produzem superfícies homeomorfas entre si. Basta "torcer" a região onde foram removidas as tampas (lembre-se que esse tipo de deformação é possível em superfícies abstratas!) e trocar as letras no final. |
|
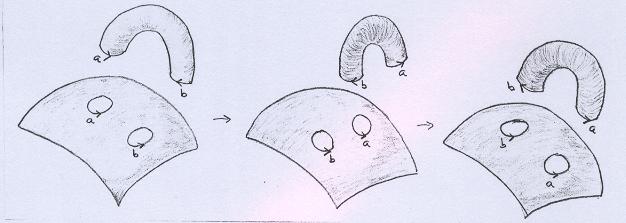
O mesmo vale para as maneiras (i) e (ii), mas isso é um pouco menos evidente. Veja primeiro que em (i) colamos a alça "por cima" e em (ii) colamos "por baixo". |

|
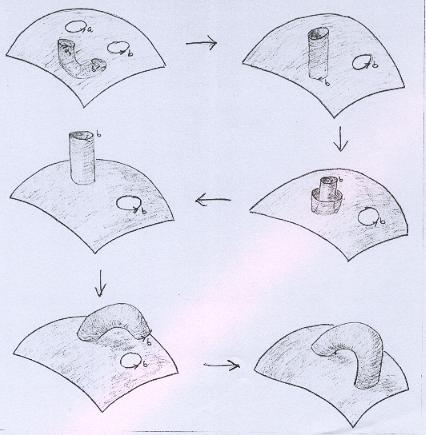
A seqüência abaixo ilustra a equivalência entre (i) e (ii). Posicionamos a alça "por baixo", colamos apenas um dos lados, "invertemos" o cilindro trazendo-o para cima e colamos a outra componente de bordo. |
|
Observe que esse mesmo raciocínio também serve para demonstrar a equivalência entre (iii) e (iv). Concluímos então de tudo isso que essencialmente só há duas maneiras de se colar alças. Essas duas maneiras nem sempre geram resultados equivalentes: se a superfície S é a esfera, por exemplo, de (i) ou (ii) obtemos um toro, e de (iii) ou (iv) obtemos a Garrafa de Klein. |
|
CapXII-pg3 |
|