|
|
CapXII-pg2 |
|
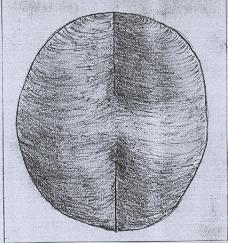
Desenvolveremos agora algumas idéias envolvendo somas conexas que nos serão úteis para obter uma classificação das superfícies. Começaremos por mostrar a seguinte afirmação: a Garrafa de Klein é (homeomorfa a) a soma conexa de dois Planos Projetivos. |
A soma conexa de dois Planos Projetivos não é uma superfície mergulhável, mas pictoricamente podemos representá-la assim: |

|
O que surpreende é que não há semelhança, à primeira vista, entre a superfície acima e a Garrafa de Klein. Acontece que homeomorfismos entre superfícies muitas vezes são "traiçoeiros", e daqui em diante veremos cada vez mais o quanto nossa intuição pode ser superada pelo uso organizado de pensamentos abstratos. |
O que faremos agora é semelhante à argumentação do Capítulo X, onde mostramos que o Plano Projetivo é obtido pela identificação dos bordos de uma Faixa de Moebius e de um Disco. Agora veremos que a Garrafa de Klein pode ser obtida pela identificação dos bordos de duas Faixas de Moebius. Isto prova o que queríamos, pois para somar os dois Planos Projetivos temos que remover uma tampa de cada um, transformando-os em Faixas de Moebius, e depois identificar os bordos. |
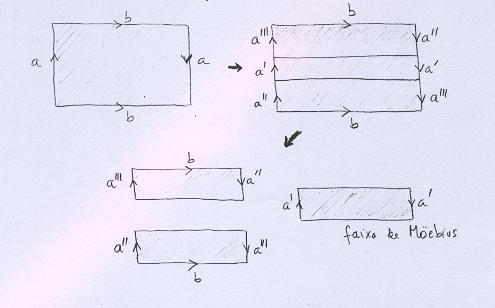
Olhamos para a Garrafa de Klein como um retângulo com lados opostos identificados, e então recortamos uma faixa horizontal central. |
|
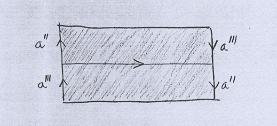
Observe que o retângulo central é uma Faixa de Moebius, após a identificação. Os outros dois retângulos podem ser colados através de b, e obtemos outra Faixa de Moebius. |
|
|
CapXII-pg2 |
|