|
|
CapXII-pg1 |
|
Começaremos este Capítulo por uma definição. |
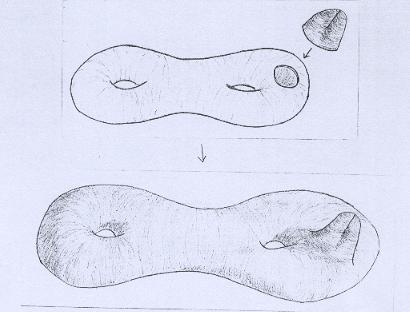
Sejam A1 e A2 duas superfícies quaisquer, ambas sem bordo. Então construímos uma terceira superfície A, a qual chamamos de soma conexa de A1 com A2 e denotamos por A = A1 # A2. A superfície A é assim definida: |
(1) Tiramos uma tampa de cada uma das superfícies. Daí resultam duas superfícies Ã1 e Ã2, cada uma com uma componente de bordo. |
(2) Colamos Ã1 e Ã2 pelos bordos, isto é, identificamos os bordos de Ã1 e Ã2. |
Por exemplo, se A1 é o bitoro e A2 é o Plano Projetivo, então Ã1 # Ã2 é a superfície mostrada abaixo. |

|
Observe também que a soma conexa de uma superfície A qualquer com a esfera é sempre homeomorfa a A. Isso porque quando tiramos uma tampa da esfera, obtemos um disco. Aí tiramos uma tampa de A (um disco) e colamos um disco no lugar. Ou seja, nada mudou! |
|
CapXII-pg1 |
|