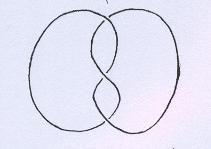
|
|
CapXI-pg2 |
|
Mostraremos agora que a resposta à pergunta é afimativa: todo nó tem uma superfície de Seifert (e todo enlace também). Esse fato foi descoberto por Herbert Seifert em 1934. |
Exemplificaremos o método usando o nó trifólio. O leitor poderá facilmente generalizar para outros nós. |
A primeira etapa é escolher uma projeção do nó. Escolhemos esta. |
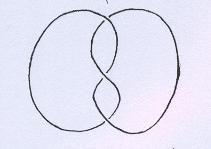
|
O segundo passo é escolher uma orientação para a linha de bordo (com enlaces basta escolher uma orientação para cada componente). |
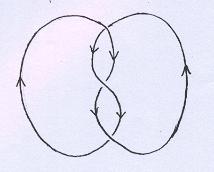
|
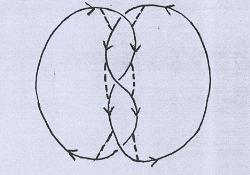
Agora adotamos a seguinte regra: em cada cruzamento, ligamos os segmentos que "entram" aos segmentos adjacentes que "saem". |
|
"Recortamos" o desenho.... |
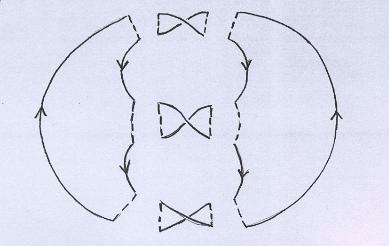
|
Então fazemos com que cada pedaço do recorte forme o bordo de um pedaço de superfície, se completarmos com as linhas pontilhadas. Neste exemplo, especificamente, teremos dois discos e três faixas torcidas. |
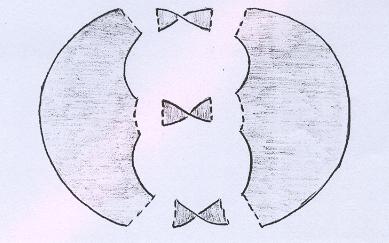
|
Agora colamos os pedaços. Pronto! |
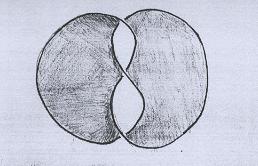
|
O leitor pode facilmente verificar que esta superfície é orientável e tem característica de Euler igual a -1. |
E se usássemos outra projeção do mesmo nó trifólio? Por exemplo, a projeção mais clássica? |
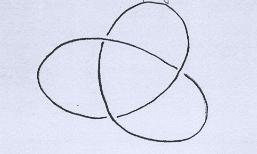
|
Orientamos o nó, identificamos os cruzamentos e os cortes, com as linhas imaginárias. |
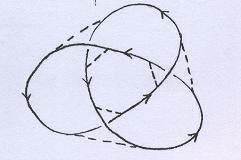
|
Em seguida cortamos e completamos com superfícies os pedaços... |
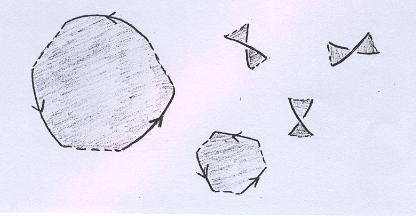
|
Então colamos. Para isso, temos que posicionar o disco menor ligeiramente acima do maior, para só depois encaixar as três tiras. |
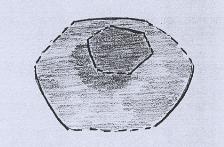
|
A superfície resultante tem o aspecto seguinte. |
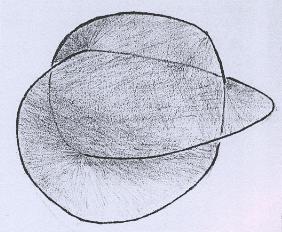
|
Sua característica de Euler também é igual a -1. |
O curioso é que podemos criar uma bonita superfície (não-orientável) com auto-interseção, colando a figura acima com a faixa triplamente torcida que tem o mesmo bordo. A característica de Euler da superfície resultante é igual a zero. Será que ela é homeomorfa à Garrafa de Klein? A resposta virá no Capítulo XIII..... |
|
CapXI-pg2 |
|