|
|
CapXI-pg1 |
|
Este Capítulo é um pequeno descanso antes dos três últimos. Aqui apresentaremos um jeito de se criar superfícies com bordo a partir dos nós e enlaces. Com uma boa tabela de nós e enlaces, teremos uma inesgotável fonte de novos exemplos de superfície para analisar. |
No próximo Capítulo falaremos um pouco mais sobre colagem de superfícies, mais ou menos como foi feito no Capítulo VII. Depois, no Capítulo XIII, enunciaremos o Teorema de Classificação das Superfícies e no Capítulo XIV estudaremos as razões que estão por trás desse Teorema. |
Aqui nos propomos a responder à seguinte pergunta: Dado um nó no espaço ambiente, será possível encontrar uma superfície orientável mergulhada (isto é, sem auto-interseção) cujo bordo é exatamente esse nó? |
Ou seja, estamos procurando superfícies orientáveis com bordo, e esse bordo deve ter uma única componente, coincidente com o nó especificado. |
Dado um nó N, se houver tal superfície ela será chamada de uma superfície de Seifert do nó N. |
A mesma pergunta pode, é claro, ser adaptada para enlaces, ao invés de nós. Nesse caso, se o enlace tiver n componentes, então procuramos por superfícies orientáveis com n componentes de bordo, cada uma delas coincidindo com uma das componentes do enlace. |
Lembremos que já comentamos, ao longo dos capítulos anteriores, alguns exemplos de superfícies (orientáveis ou não) cujos bordos formam nós e enlaces não triviais. Primeiro, vimos uma superfície não-orientável cujo bordo é o nó trifólio, e mostramos uma isotopia desse bordo com a forma mais clássica do nó trifólio. |

|
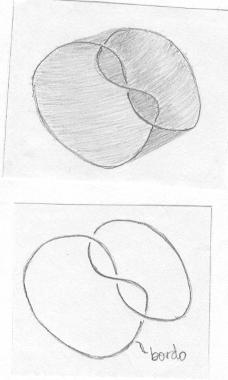
Também vimos uma superfície orientável cujo bordo tem duas componentes formando um enlace de Hopf. Vimos que essa superfície é homeomorfa (mas não isotópica) ao cilindro. |
|
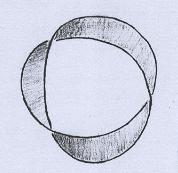
Também vimos que podemos produzir superfícies com faixas torcidas. Uma faixa colada com três meias-torções resulta numa superfície como a mostrada abaixo (exceto pelo fato de que tiras de papel não se dobram exatamente como desejamos). |
|
Observe que esta é outra superfície não orientável cujo bordo é o nó trifólio. De fato ela é isotópica à anterior. Acompanhe na animação abaixo. |

|
|
CapXI-pg1 |
|