|
|
CapX-pg4 |
|
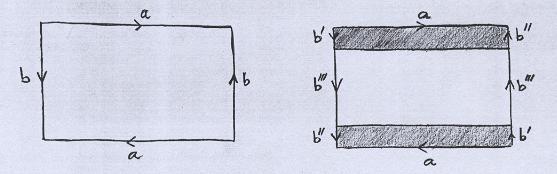
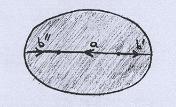
Agora notemos um fato muito importante: o Plano Projetivo resulta da colagem de uma Faixa de Moebius com um Disco. |
Para ver isso, desenhamos o retângulo do Plano Projetivo com os segmentos a serem identificados e isolamos duas faixas próximas dos segmentos inferior e superior. As faixas são escolhidas de tal modo que elas se encaixam, se as laterais forem coladas. Indicamos isso com os símbolos b' e b''. |

|
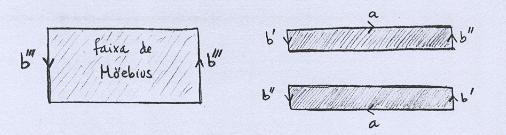
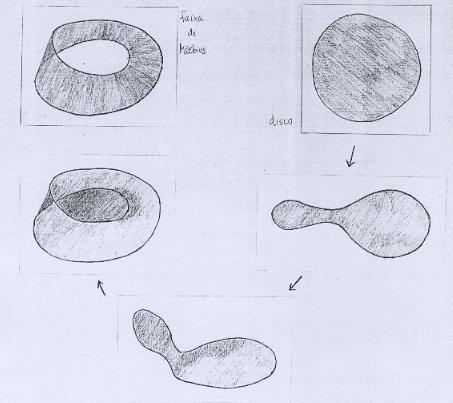
Então recortamos as faixas, ficando com três peças, umas das quais é a Faixa de Moebius. |
|
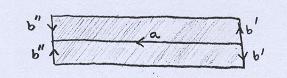
As duas peças restantes podem ser coladas ao longo de a. Para isso, invertemos a de cima, para que as orientações coincidam. |
|
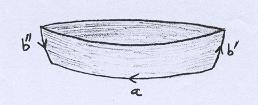
Em seguida colamos ao longo de b' e b'', obtendo uma espécie de "barquinho". |
|
Mas o "barquinho" é isotópico ao Disco. |
|
Podemos também colar a Faixa de Moebius ao Disco diretamente no espaço ambiente. O que fazemos é deformar o Disco, de forma que seu bordo fique exatamente igual ao da Faixa de Moebius usual. |
|
Aí é só colar! Essa é uma boa maneira de se entender o Plano Projetivo, mas é um pouco mais difícil visualizar os pontos de auto-interseção da superfície. |
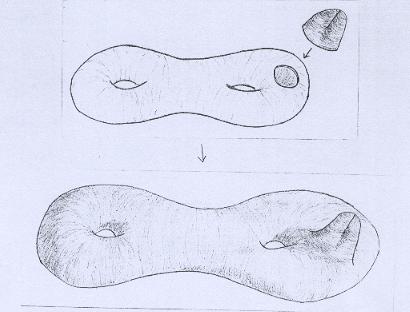
A idéia de que um Plano Projetivo é uma Faixa de Moebius mais um Disco ou, de maneira inversa, que a Faixa de Moebius é um Plano Projetivo menos uma tampa, ajuda a ilustrar o acréscimo de Faixas de Moebius a superfícies das quais uma tampa é retirada. Isso será de grande valia mais adiante. Vejamos um exemplo. |
|
Na figura acima, colamos uma Faixa de Moebius a um bitoro sem uma tampa. Podemos nos perguntar qual é a característica de Euler dessa superfície. Sabemos que a característica de Euler do bitoro é X=-2. Tirando uma tampa, a característica de Euler passa a ser de X-1, isto é, -3. Por outro lado, a característica de Euler da Faixa de Moebius é zero. O leitor pode então verificar, baseado nas idéias do Capítulo VII, que a superfície resultante tem característica de Euler X-1, ou seja, depois de retirada a tampa, ela não muda com o acréscimo da Faixa de Moebius. |
Outro exemplo: a esfera tem X=2. Removendo-se uma tampa, ela vira um disco, com X=1. Colando uma Faixa de Moebius a característica de Euler permanece igual a 1, e a superfície resultante é um Plano Projetivo, confirmando nossos cálculos. |
|
CapX-pg4 |
|