
|
|
CapIX-pg6 |
|
Podemos calcular a caracter�stica de Euler em superf�cies definidas via identifica��o, mas devemos tomar cuidado na contagem de v�rtices e arestas. Faremos isso primeiramente para a Esfera, o Cilindro, o Toro e a Faixa de Moebius, para confirmar os n�meros obtidos, e depois passaremos � Garrafa de Klein e ao Plano Projetivo. |
Esfera. Definimos a esfera pela identifica��o do bordo de dois discos. Introduzimos uma triangula��o que seja compat�vel no bordo dos discos. |

|
Numerando faces, arestas e v�rtices, tomando cuidado com o fato de que h� v�rtices e arestas que aparecem duas vezes no desenho, mas devem ser contados uma s� vez, pois s�o identificados na colagem! Temos F=6, A=9 e V=5, e portanto X=2. Se o leitor ainda n�o acredita que a caracter�stica de Euler n�o depende da triangula��o, experimente calcular com outra! |
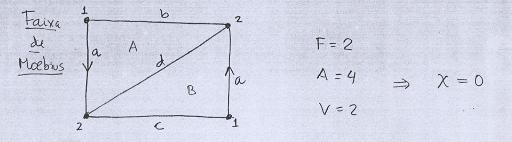
As pr�ximas cinco superf�cies s�o obtidas a partir da identifica��o dos lados de um ret�ngulo. No ret�ngulo, o desenho da triangula��o � sempre o mesmo, mas a maneira como os v�rtices e arestas s�o contados muda de um caso para o outro, por causa das particularidades de cada colagem. |

|
|

|

|

|
Em suma, a caracter�stica de Euler da Garrafa de Klein � zero (assim como o Toro, o Cilindro e a Faixa de Moebius) e do Plano Projetivo � 1. |
O Plano Projetivo tamb�m n�o � orient�vel e n�o pode ser inserido no espa�o ambiente sem auto-interse��o. Falaremos sobre isso no pr�ximo Cap�tulo! |
|
CapIX-pg6 |
|