|
|
CapX-pg1 |
|
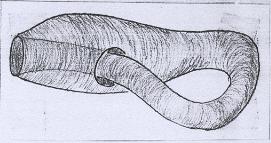
Como vimos no Capítulo anterior, há superfícies definidas via identificação que não podem ser desenhadas no espaço ambiente sem auto-interseção. O exemplo que mostramos foi a Garrafa de Klein. |
Observe que poderíamos evitar a auto-interseção se removêssemos da Garrafa de Klein uma tampa, como mostra a figura abaixo. |

|
Esse é, no entanto, um caso excepcional. O Plano Projetivo, por exemplo, não pode ser desenhado sem auto-interseção mesmo que removamos um número qualquer de tampas! |
Antes porém de falarmos no Plano Projetivo, vejamos como interpretar as superfícies com auto-interseção, sem fugir ao espírito do que vimos dizendo até agora. |
No Capítulo IX vimos que podemos abstrair a noção de superfície, independentemente do espaço ambiente, através da colagem de um ou mais pedaços do plano. A especificação e a orientação dos segmentos a serem colados define a superfície, de um ponto de vista que considera iguais todas as superfícies homeomorfas entre si. |
Define também quem são as vizinhanças de cada ponto, e se são pontos interiores ou de bordo. A realização da colagem no espaço ambiente é chamada de mergulho, se ocorrer sem auto-interseção. |
Como já vimos, em geral há várias maneiras de se mergulhar uma superfície no espaço ambiente. Além disso, dois mergulhos de uma mesma superfície podem não ser isotópicos entre si, mas sempre são homeomorfos: basta recortar uma das superfícies exatamente onde foi feita a colagem e depois colar como a outra (obs: a esfera é a única superfície mergulhável sem bordo em que dois mergulhos são necessariamente isotópicos entre si). |
Não falaremos aqui de isotopias que envolvam superfícies com auto-interseção. Também não imporemos regras para desenhá-las. Esse tipo de superfície servirá apenas como uma maneira tosca de representarmos no espaço uma definição feita abstratamente no plano. A definição feita no plano, no entanto, deve seguir as regras definidas no Capítulo anterior! |
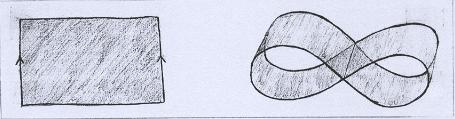
É interessante observar que mesmo superfícies mergulháveis poderiam ser coladas com alguma auto-interseção. Por exemplo, o cilindro... |
|
Devemos no entanto saber interpretá-las corretamente, à luz do Capítulo IX e não mais do Capítulo II. A maneira errada de se pensar é considerar um ponto da interseção como um único ponto e tomar uma vizinhança dele como sendo o conjunto de pontos da superfície dentro de uma pequena bola ao seu redor, que neste caso teria o seguinte aspecto: |

|
Esse seria o ponto de vista do Capítulo II, mas lá não permitíamos as auto-interseções! Daquele ponto de vista essa vizinhança é proibida, pois não é homeomorfa a um disco. |
A maneira certa de pensar sempre deve fazer uso da definição da superfície via identificação de pedaços do plano. No exemplo acima, dois segmentos do retângulo se encontram no espaço, e a cada ponto da auto-interseção correspondem dois pontos do retângulo. |

|
Cada um desses pontos tem uma vizinhança em forma de disco, à qual corresponde um disco na colagem. Então os pontos da auto-interseção no espaço devem ser vistos como pares de pontos onde cada um deles tem sua própria vizinhança, definida antes da colagem! |
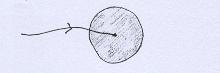
Observe que para que Aderbal atinja um ponto, em algum momento ele precisa entrar em sua vizinhança. |
|
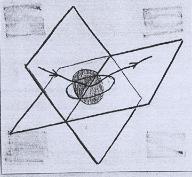
Se levarmos isso em conta, perceberemos que não podemos "pular" de uma vizinhança para outra, deste modo: |
|
Olhado no retângulo, esse caminho seria: |
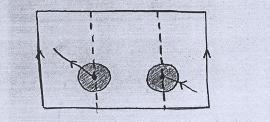
|
Por exemplo, se Aderbal quiser ir do ponto A ao ponto B, como ilustrado na figura abaixo, ele terá que dar a volta! |
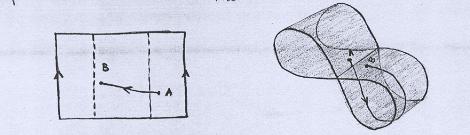
|
Na Garrafa de Klein ocorre algo semelhante. As linhas pontilhadas no retângulo coincidirão após a colagem, dando a falsa impressão de que os pontos A e B estão próximos! |
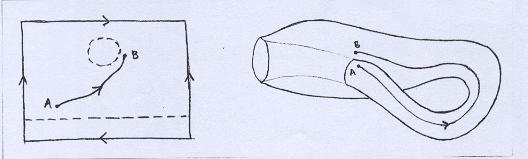
|
|
CapX-pg1 |
|