|
|
CapIX-pg3 |
|
Estamos portanto afirmando que uma superfície pode ser definida a partir da colagem, que se constitui na identificação de segmentos de bordo, ou mesmo componentes de bordo inteiras, de uma ou mais superfícies. No caso do cilindro, por exemplo, a identificação é feita entre pares de lados de um retângulo, que é uma figura plana. |
Vimos também que as instruções de colagem não informam exatamente como a colagem deve ser feita no espaço, apenas quais segmentos ou curvas devem ser colados, respeitando uma determinada orientação. No entanto, todas as superfícies obtidas serão sempre homeomorfas entre si. |
Tudo isso parece um pouco contraditório, pois afirmamos ao mesmo tempo que as superfícies se definem através da colagem, porém por outro lado elas não estão precisamente definidas, uma vez que várias superfícies diferentes podem ser construídas de acordo com a escolha que fazemos de sua posição no espaço. |
A contradição deixa de existir, entretanto, se passarmos a encarar as superfícies não da forma como fizemos no Capítulo II, isto é, como um conjunto bidimensional no espaço, mas sim do mesmo modo como entendemos os nós no Capítulo III. Em outras palavras, consideraremos duas superfícies equivalentes, ou mesmo iguais, se elas são homeomorfas. Assim, a forma como as colocamos no espaço é apenas uma maneira de visualizá-las, sendo todas as outras formas igualmente válidas. |
Lembremos no entanto que toda superfície era formada somente por pontos interiores ou de bordo, isto é, pontos cujas vizinhanças eram isotópicas a um disco com o ponto no centro ou na fronteira do disco. Para isso, tivemos que definir o que é a vizinhança de um ponto na superfície, usando bolinhas no espaço ambiente. Se, porém, definimos uma superfície sem nos importarmos com sua disposição espacial, como por exemplo o toro formado pela identificação dos lados de um retângulo, de que maneira definiremos as vizinhanças dos pontos? |
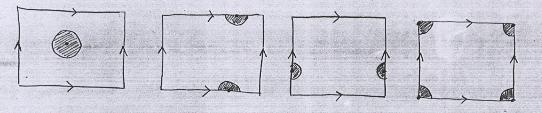
Teremos que definir essas vizinhanças sem usar o espaço ambiente. Vejamos no exemplo do toro, que é bastante ilustrativo. Na figura abaixo definimos as vizinhanças de alguns pontos: são pedaços de discos, às vezes desconectados, que se juntam depois que for feita a colagem. |

|
Observe que todos os vértices do retângulo são identificados, representando um ponto só do toro. Os quatro pedacinhos de disco se juntam, formando a vizinhança do ponto no toro. |
No caso do cilindro há ainda pontos de bordo, e para eles as vizinhanças são semi-discos, às vezes fragmentados. |

|
O importante a se lembrar é que, mesmo que as vizinhanças sejam formadas por vários pedaços, ao se fazerem as identificações esses pedaços devem se colar de tal forma que a vizinhança fique isotópica a um disco. Se o ponto for interior, ficará no centro do disco, e se for de bordo, ficará em sua fronteira. |
|
CapIX-pg3 |
|