|
|
CapIX-pg2 |
|
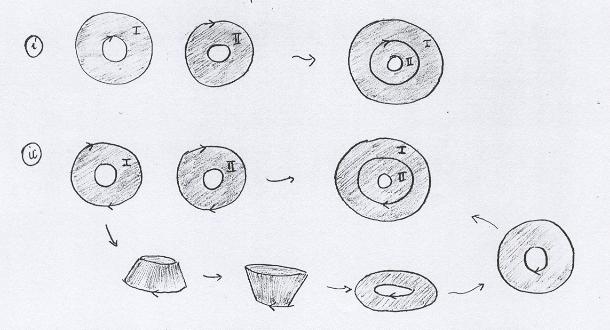
Vejamos mais algumas colagens, a título de ilustração. Os segmentos a serem colados são orientados com setas. |
Colagem de dois anéis por um dos bordos. |

|
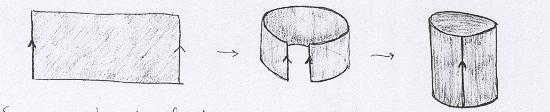
Colagens que só envolvem uma peça. Isso também pode ser feito, por exemplo um retângulo em que colamos as laterais forma um cilindro. |
|
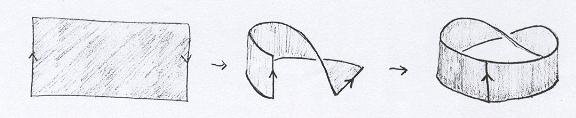
Aqui o sentido das setas é importante. Se elas estiverem em sentidos opostos, então a superfície resultante é uma Faixa de Moebius. |
|
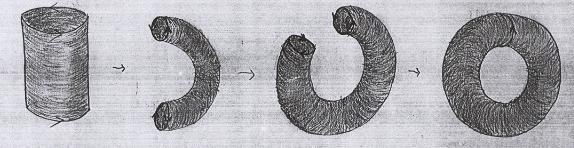
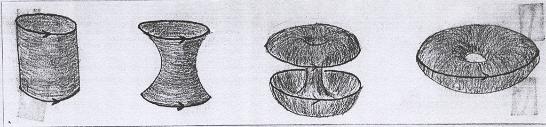
Outro exemplo vem do cilindro, colando-se suas duas componentes de bordo e formando o toro. |
|
Veja outra maneira de colar para obter o toro. |
|
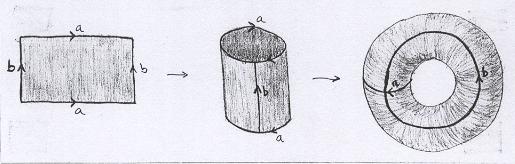
Como o cilindro foi feito a partir do retângulo, podemos dizer que o toro é um retângulo onde colamos os pares de lados opostos. |
|
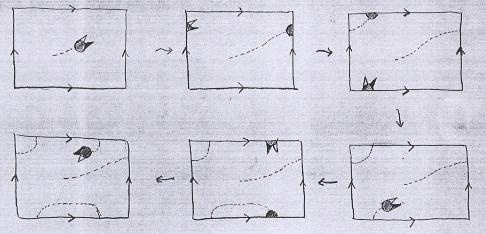
Veja que tivemos que usar letras para ficar claro quais lados devem se colar. No jargão matemático diz-se que os lados que serão colados são identificados. Significa que consideramos o par de segmentos como um segmento só: por exemplo, se a trajetória de Aderbal se encontra com o segmento do lado direito, então ela prossegue naturalmente do lado esquerdo; se encontra com o segmento de cima, continua no lado de baixo. |
|
Isso nos sugere uma nova forma de se definir uma superfície, através de colagens, em que não nos preocupamos em como ela é colada mas só aonde. No caso do toro, a colagem no espaço poderia ter sido feita de modo diverso: |

|
Duas colagens feitas diferentemente no espaço são, no entanto, sempre homeomorfas entre si. |
|
CapIX-pg2 |
|