CapVIII-pg6

CapVIII-pg7

CapIX-pg1

 

Uma tira colada após três meias-torções produz uma superfície não-orientável e com uma componente de bordo. Esse bordo é o nó trifólio! Verifique!! Observe também que a superfície (......), mostrada anteriormente, é isotópica a uma tira com três meias-torções!

 

Pode-se mostrar que: 1) Uma tira colada após um número par de meias-torções é uma superfície orientável com duas componentes de bordo, e é homeomorfa ao cilindro. No entanto, se duas dessas superfícies são formadas por um número diferente de torções, então elas não são isotópicas entre si. 2) Uma tira colada após um número ímpar de meias-torções é uma superfície não-orientável com uma componente de bordo, e é homeomorfa à Faixa de Moebius. No entanto, se duas dessas superfícies são formadas por um número diferente de meias-torções, então elas não são isotópicas entre si. (PERGUNTA A RESPONDER: ISOTOPIA OU NÃO SE APENAS O SENTIDO DAS TORÇÕES É TROCADO!)

 

Propriedade de Jordan. Finalmente, queremos saber se as superfícies produzidas por tiras torcidas têm ou não têm a propriedade de Jordan. O cilindro, como já vimos, tem a propriedade de Jordan: toda curva fechada sem auto-interseções separa o cilindro em dois pedaços.

 

Sendo a propriedade de Jordan um invariante, o mesmo deve valer para qualquer superfície com um número par de meias-torções, pois todas elas são homeomorfas ao cilindro!

 

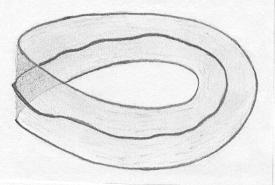
E a Faixa de Moebius? O leitor é convidado a fazer uma com papel e cortá-la usando uma tesoura, ao longo de um caminho desorientador como abaixo. Observe que esse caminho desorientador é também uma curva não retrátil.

 

O resultado surpreende os desavisados: a Faixa de Moebius não se separa em dois pedaços! Isso indica que ela não tem a propriedade de Jordan, ao contrário do cilindro. E a superfície resultante é uma tira com duas meias-torções, portanto, segundo vimos, orientável e com duas componentes de bordo.

 

Em geral temos que: Uma superfície com um número par de meias-torções, quando cortada ao longo de uma curva fechada, sem auto-interseções, não retrátil, dá origem a duas superfícies, cada uma com o mesmo número de torções da curva original. Uma superfície com um número ímpar de meias-torções, quando cortada ao longo de uma curva fechada, sem auto-interseções, e que é um caminho desorientador, dá origem a uma superfície (só uma) com o dobro do número de meias-torções. Observe que o dobro de um número é sempre par, logo a nova superfície é orientável.

 

Para finalizar, observe também o que acontece com o seguinte caminho na Faixa de Moebius, que não é desorientador. Cortando a Faixa ao longo dele, resultam duas superfícies: uma é uma Faixa de Moebius e a outra é uma superfície de duas meias-torções.

 

CapVIII-pg6

CapVIII-pg7

CapIX-pg1