|
|
CapVIII-pg6 |
|
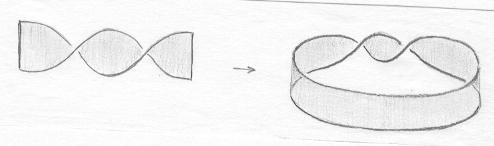
E se torcermos mais ainda a tira de papel, por exemplo, se fizermos duas meias-torções? |

|
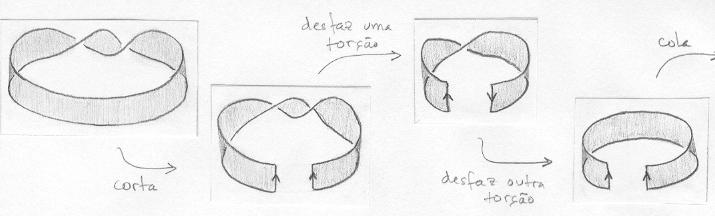
Essa superfície é orientável e tem duas componentes de bordo, como o cilindro. Ela é homeomorfa ao cilindro: basta recortá-la, destorcê-la duas vezes e colar no mesmo lugar. Observe que não podemos destorcê-la apenas uma vez e colar, pois não estaríamos respeitando o sentido das setas. |
|
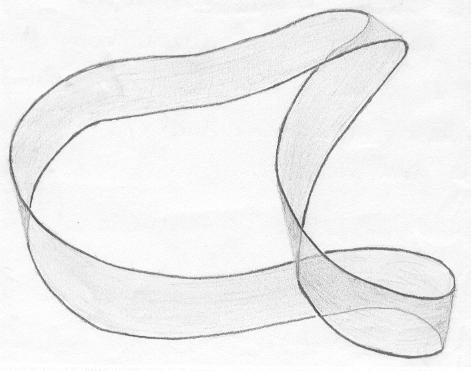
Essa superfície, quando feita em papel com uma tira suficientemente comprida (em relação a sua largura), assume o aspecto da figura abaixo. |
|
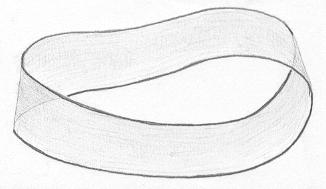
Ou senão da figura abaixo. |
|
A superfície de duas torções, no entanto, apesar de ser homeomorfa ao cilindro, não é isotópica ao cilindro. Não é possível transformá-la no cilindro somente com deformações. Podemos ver isso examinando o bordo das duas. |
O bordo do cilindro tem duas componentes, formando um enlace trivial. Já a superfície de duas torções tem um bordo assim: |
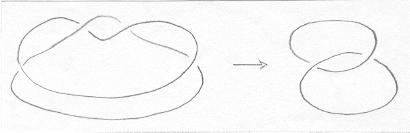
|
Esse enlace é o enlace de Hopf, e é sabido que ele não pode ser desmanchado por isotopias a ponto de virar um enlace trivial. Se existisse uma isotopia que transformasse a superfície de duas torções num cilindro, ela deveria automaticamente transformar o enlace de Hopf num enlace trivial, o que é impossível. Logo tal isotopia não existe! |
Se o leitor não estiver distraído irá lembrar que fizemos a mesma argumentação um pouco mais para trás (...). De fato, a superfície lá mostrada é isotópica a uma tira com duas meias-torções! |
|
CapVIII-pg6 |
|