|
|
CapVII-pg4 |
|
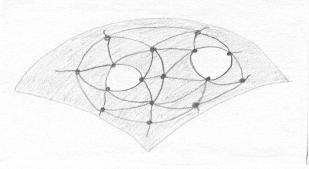
De fato, podemos acrescentar qualquer número de alças à esfera e nos perguntarmos qual será a característica de Euler da superfície resultante. Da Esfera (X=2) para o Toro (X=0) a redução foi de duas unidades. Será que é sempre assim? |
Procedemos de maneira semelhante à situação de remoção de tampas. Primeiro, localizamos as tampas e escolhemos uma triangulação compatível, tal que cada tampa seja uma face. Se a triangulação tem F faces, A arestas e V vértices, ao retirarmos as tampas restarão (F-2) faces, A arestas e V vértices. |

|
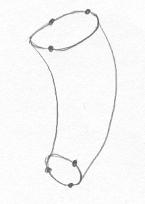
O cilindro deve encaixar nos buracos deixados pelas tampas removidas. Em cada encaixe, marcamos no cilindro onde batem os três vértices do bordo da tampa. |
|
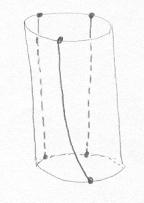
Olhando para o cilindro "endireitado", construímos um grafo com faces poligonais. Isso é feito ligando-se por arestas os vértices das duas componentes de bordo do cilindro. Ficamos com 3 faces, cada uma de quatro lados (retângulos). |
|
Esse grafo do cilindro tem Fc=3 faces, Ac=9 arestas e Vc=6 vértices. Donde Xc = Fc - Ac + Vc = 0, confirmando o que já havíamos calculado anteriormente: a característica de Euler do Cilindro é igual a zero. |
Ao juntarmos o Cilindro nos encaixes, teremos automaticamente um grafo de faces poligonais da superfície resultante. As faces sobre as alças são os retângulos sobre o Cilindro, e as faces sobre o restante são os triângulos da triangulação da superfície original. Se soubermos contar o número total de faces F', o número de arestas A' e o número de vértices V', poderemos obter a característica de Euler X'=F'-A'+V'. Então mão à obra! |
O número de faces F' é igual ao número de faces do cilindro (Fc), mais as faces da superfície original (F) menos dois, pelas duas tampas retiradas: F' = Fc + F -2. |
O número de arestas A' é igual ao número de arestas do cilindro (Ac) mais o número de arestas (A) menos 6, pois as seis arestas do bordo do cilindro já foram contadas na triangulação da superfície original. Isto é, A' = Ac + A - 6. |
Com os vértices é a mesma coisa: V' = Vc + V -6. |
Então |
|
CapVII-pg4 |
|