| 
|
|
CapVI-pg1 |
|
As propriedades intr�nsecas das superf�cies, como a conectividade simples e a propriedade de Jordan, al�m de n�o se alterarem sob isotopias, tamb�m n�o mudam quando cortamos e colamos no mesmo lugar. No jarg�o matem�tico, dizemos que essas propriedades s�o invariantes sob homeomorfismos, ou ent�o que s�o invariantes topol�gicos das superf�cies. |
Um invariante topol�gico pode ser bin�rio: a superf�cie ou tem ou n�o tem determinada propriedade. Por exemplo, ela tem ou n�o tem a propriedade de Jordan, ela � ou n�o � simplesmente conexa, etc. Pode ser tamb�m um n�mero, por exemplo o n�mero de componentes de bordo da superf�cie, ou ent�o sua caracter�stica de Euler, que definiremos a partir de agora. |
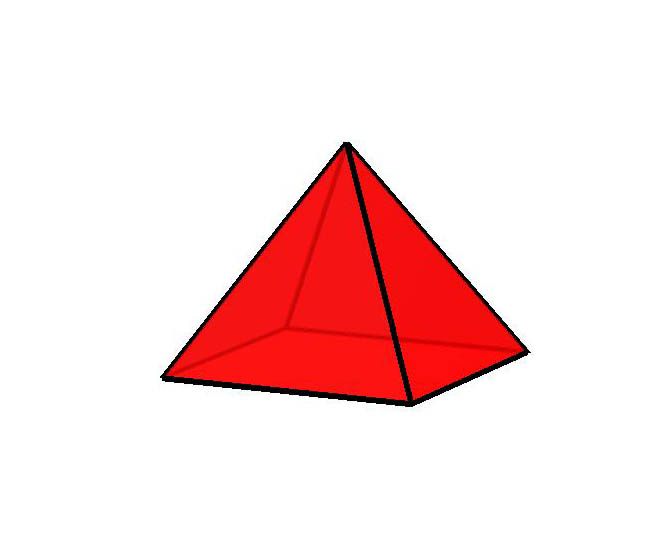
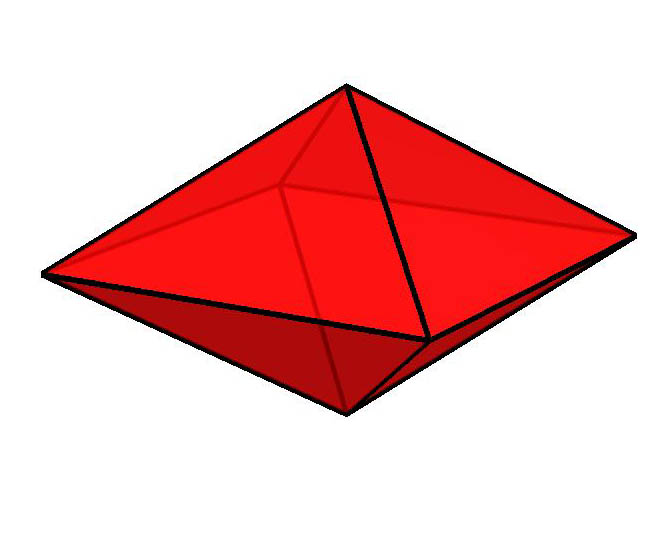
A caracter�stica de Euler se inspira no Teorema de Euler para poliedros. Observe os dois poliedros abaixo: a Pir�mide e o Octaedro. |

| 
|
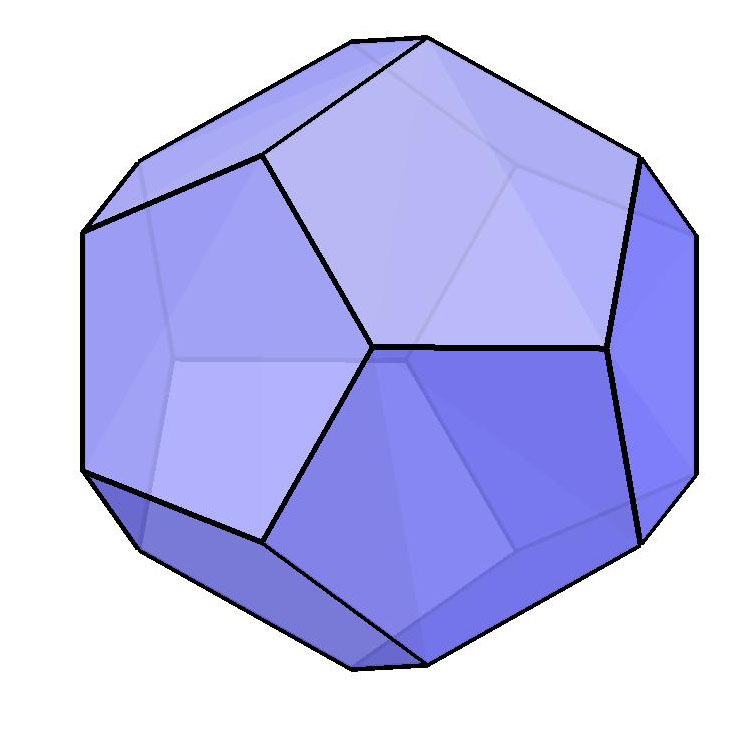
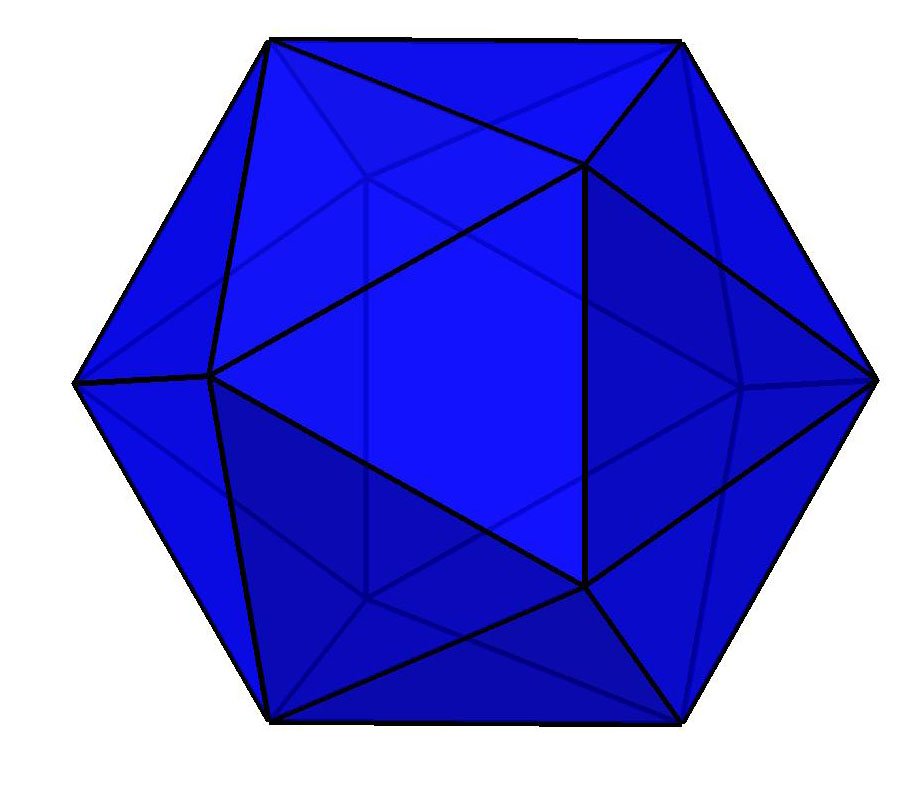
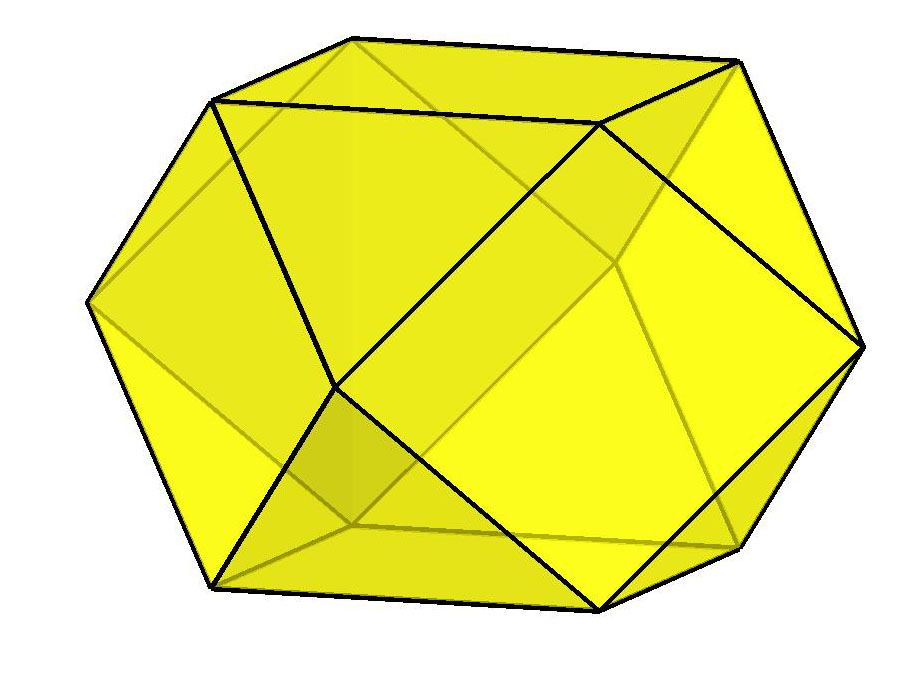
E mais outros tr�s, da esquerda para a direita: o Dodecaedro, o Icosaedro e o Cuboctaedro. |
| 
| 
|
Para cada poliedro podemos contar o n�mero de faces F, o n�mero de arestas A e o n�mero de v�rtices V. Depois calculamos o n�mero X = F - A + V. Vejamos o resultado na tabela abaixo, incluindo tamb�m o Cubo e o Tetraedro. |
| Poliedro | F | A | V | X = F - A + V |
|---|---|---|---|---|
| Cubo | 6 | 12 | 8 | 2 |
| Tetraedro | 4 | 6 | 4 | 2 |
| Pir�mide | 5 | 8 | 5 | 2 |
| Octaedro | 8 | 12 | 6 | 2 |
| Dodecaedro | 12 | 30 | 20 | 2 |
| Icosaedro | 20 | 30 | 12 | 2 |
| Cuboctaedro | 14 | 24 | 12 | 2 |
Verificamos portanto que os n�meros de faces, arestas e v�rtices variam conforme o poliedro, mas o n�mero X � sempre igual a 2! Isso � uma propriedade geral dos poliedros: tente calcular X em outros exemplos e voc� constatar� que o resultado n�o ser� diferente de 2. |
|
CapVI-pg1 |
|