|
|
CapV-pg3 |
|
Para fixar idéias, vejamos mais um exemplo de duas superfícies que não são isotópicas entre si, mas que no entanto são homeomorfas, isto é, se for possível cortar e colar no mesmo lugar, além de deformar, então conseguiremos transformar uma na outra, ao passo que só com deformações nunca conseguiríamos. |
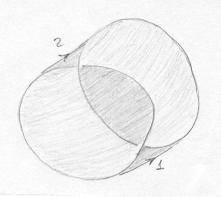
Uma das superfícies é o Cilindro. A outra é a superfície mostrada abaixo. |

|
O bordo dessa superfície tem duas componentes, que formam um enlace, o enlace de Hopf. Por outro lado, as duas componentes de bordo do cilindro não se enlaçam. Se as duas superfícies fossem isotópicas então o enlace se desfaria sem que cortássemos em nenhum lugar, o que é impossível. |
Será que cortando e colando no mesmo lugar podemos mostrar que elas são equivalentes? |
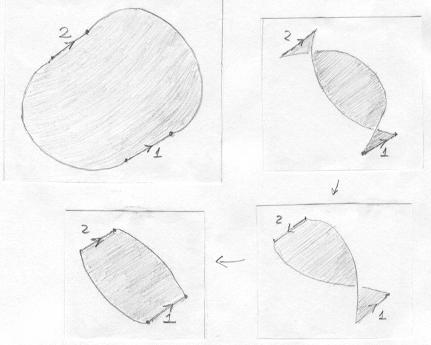
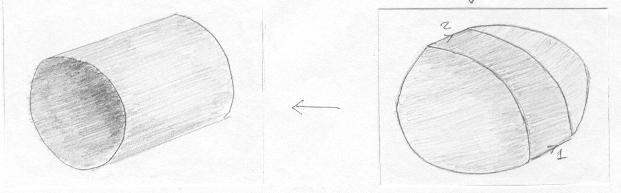
O corte é feito nos segmentos numerados 1 e 2. Observe que antes do corte colocamos uma seta de orientação em cada segmento, para não colarmos depois de forma "invertida". Depois do corte, com duas meias-torções regularizamos a tira e colamos no lugar original, mantendo coerentes os sentidos das setas. Finalmente fazemos uma isotopia e obtemos o cilindro! |
|
|
|
CapV-pg3 |
|