|
|
CapV-pg2 |
|
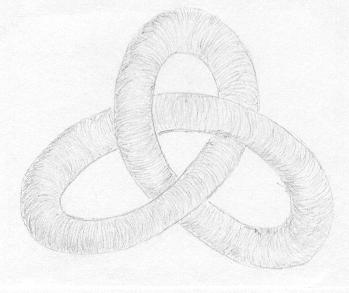
Agora examine a seguinte superfície. Observe primeiro que ela se parece com o nó trifólio, só que agora mais "gordinha". Na verdade, isso até sugere uma maneira de se construir novas superfícies, a partir dos nós. Basta enrolar um tubo de acordo com a linha que forma o nó e colar as pontas. |

|
O leitor pode se perguntar: o toro também se parece com um tubo, onde colamos as pontas, mas seu formato se parece mais com um círculo "engordado". Será que a superfície acima é isotópica a um toro? |
Se refletirmos um pouco veremos que a resposta é não! Se pudéssemos deformar a superfície acima de forma que ela se transforme num toro, então poderíamos transformar o nó trifólio num nó trivial, o que já afirmamos ser impossível (só é preciso acreditar que o nó trifólio e o nó trivial não são isotópicos, mas isso já é outra história...). |
No entanto há ainda algo na superfície que a faz parecer um toro. Qual será o ponto de vista dos habitantes da superfície? |
Imagine por exemplo Aderbal habitando essa superfície. Será que ele, dentro dela, pode fazer algum experimento e perceber alguma diferença em relação ao toro? Lembremos que ele é um ser bidimensional e só é capaz de enxergar objetos bidimensionais, localizados dentro da superfície. Na analogia que fizemos com as lâminas de vidro, é como se o vidro fosse opaco, e assim ele não pode enxergar a maneira como sua superfície está enrolada no espaço. |
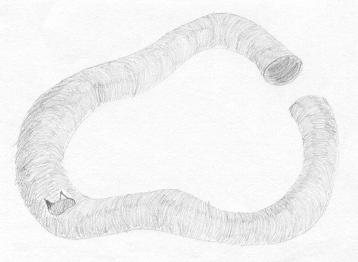
Se nós por exemplo cortarmos a superfície em algum lugar longe das vistas de Aderbal, desfizermos o nó e emendarmos novamente, no mesmo lugar, Aderbal nunca se dará conta do que aconteceu! |

|
|

|
O que temos então são duas superfícies que não são equivalentes do ponto de vista da isotopia, mas que passam a ser se, além de deformações, nos permitirmos recortar a superfície e depois colar no mesmo lugar. Esse tipo de transformação das superfícies é chamado de homeomorfismo. |
|
CapV-pg2 |
|