|
CapIV-pg2 |
|
Se o toro e a esfera são superfícies não isotópicas entre si, mas têm o mesmo número de componentes de bordo (isto é, zero), então podemos nos perguntar se há algum outro tipo de propriedade intrínseca das superfícies que as distinga. |
Discutiremos, ainda somente com a ajuda dos exemplos mencionados até agora, duas delas: a propriedade de Jordan e a conectividade simples. Usaremos um pouco os préstimos de Aderbal para essa investigação do mundo bidimensional. |
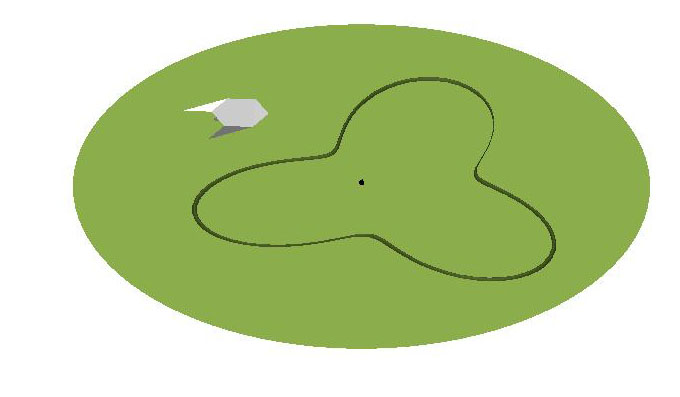
Olhemos para o disco, e consideremos nele uma curva fechada, que não se auto-intersecte. Aderbal quer chegar no ponto preto, mas para isso é obrigado a atravessar a curva. A curva é, no entanto, uma barreira intransponível para Aderbal (lembre-se de que é preciso ter uma porta em cada relógio para se poder ver as horas!). |

|
O que acontece é que a curva acabou por dividir o disco em duas regiões. Se Aderbal está em uma delas, só poderia chegar à outra atravessando a curva, mas isso ele não faz porque não é um fantasma! |
Se recortássemos a superfície ao longo dessa curva, ficaríamos com dois pedaços: um deles isotópico a um anel e outro isotópico a um disco. |
É intuitivo perceber que qualquer curva fechada sem auto-interseção no disco o delimita em duas regiões. Será que o mesmo vale para outras superfícies? |
Para a Esfera, sim! Qualquer curva fechada sem auto-interseção a separa em dois pedaços, só que agora ambos os pedaços são isotópicos a um disco. |
E no Anel? No Anel também é verdade, mas temos que considerar dois tipos de curvas: as que circundam e as que não circundam o buraco central. Se a curva circunda, do recorte saem dois anéis, ... |
... e se não circunda, saem um disco e uma superfície que é um disco menos duas tampas (que é uma superfície com três componentes de bordo). |
Dizemos que a Esfera, o Disco e o Anel são superfícies de Jordan, ou ainda, que satisfazem à propriedade de Jordan: qualquer curva fechada sem auto-interseção as separa em dois pedaços. |
Podemos introduzir uma nomenclatura, dizendo que uma se uma curva fechada sem auto-interseção separa a superfície em dois pedaços então ela é uma curva de Jordan. Sendo assim, numa superfície de Jordan todas as curvas fechadas sem auto-interseção são necessariamente curvas de Jordan! |
E então nos perguntamos: será que o Toro é uma superfície de Jordan? Em outras palavras, será que todas as curvas fechadas sem auto-interseção, desenhadas no Toro, são curvas de Jordan? |
Os dois exemplos abaixo mostram que não: há curvas no Toro que não o dividem. Se recortarmos o Toro ao longo delas, obteremos uma superfície isotópica a um cilindro. |
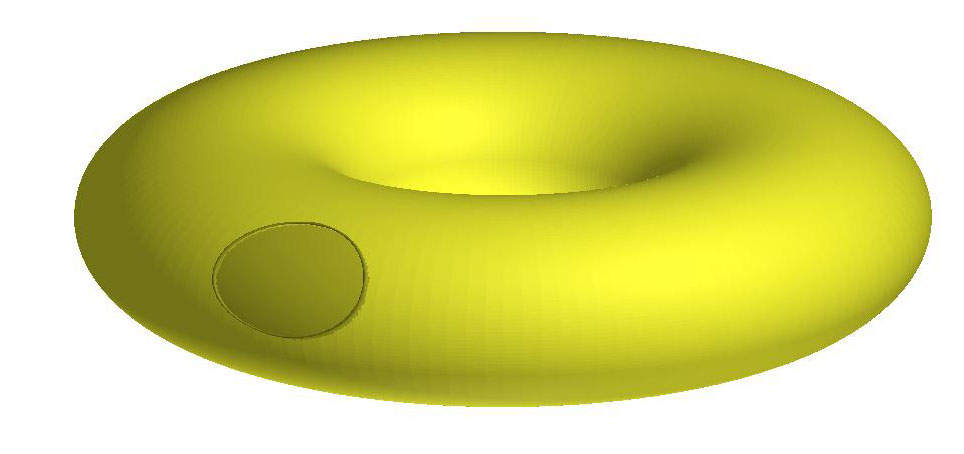
Mesmo que o Toro não seja uma superfície de Jordan ele pode, entretanto, ter curvas de Jordan, como mostra o exemplo abaixo. A curva mostrada divide a superfície em dois pedaços, o mais escuro e o mais claro. Aliás, toda superfície tem curvas de Jordan, mas a superfície só é de Jordan se todas as curvas nela contidas são de Jordan! |
|
|
CapIV-pg2 |
|