|
|
CapIV-pg1 |
|
Como dissemos, adotaremos aqui o ponto de vista da Topologia, considerando sempre equivalentes as superfícies que se podem transformar umas nas outras através de uma deformação. E nos concentraremos em estudar justamente as propriedades das superfícies que não se alteram com essas deformações, que serão chamadas de propriedades topológicas. Dito de outra forma, duas superfícies partilham das mesmas propriedades topológicas se elas são equivalentes entre si por deformações. |
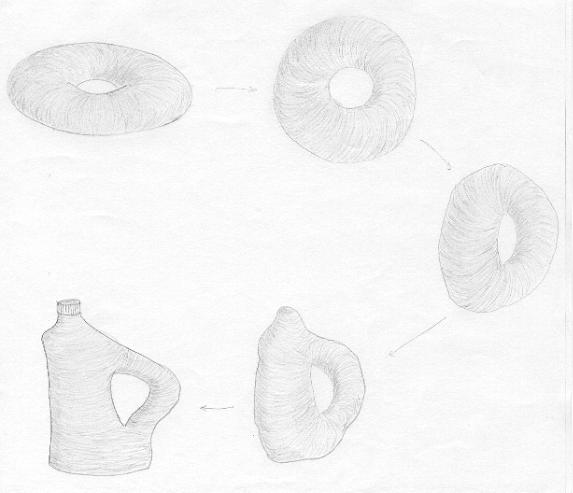
Deformações de superfícies e nós no espaço são chamadas de isotopias. Vejamos alguns exemplos. |
Nesta primeira, vemos que um toro é equivalente ao formato de uma garrafa d'água (daquelas em que a água pode entrar pela alça). |

|
Aqui vemos que o cone e o disco são equivalentes! |
O mesmo acontece entre o cilindro e o anel. |
Ou ainda, entre o cubo e a esfera! |
Por outro lado, tente o leitor verificar se é possível deformar o anel para que se transforme num disco e verá que não é! Realmente, o anel tem duas componentes de bordo e o disco só tem uma, e não é possível mudar o número de componentes de bordo somente com deformações. Por essa razão, também a esfera não pode ser isotópica nem ao disco nem ao anel, pois não tem nenhuma componente de bordo (se aparecesse uma componente de bordo na deformação da esfera estaríamos violando a regra de que é proibido "rasgar" a superfície!). |
Esse argumento que usa o número de componentes de bordo como critério para saber se duas superfícies são ou não são isotópicas entre si só serve para negações. Ou seja, se duas superfícies não têm o mesmo número de componentes de bordo então podemos concluir que elas não são equivalentes. No entanto, o contrário não é verdadeiro: não podemos dizer que duas superfícies são equivalentes só porque elas têm o mesmo número de componentes de bordo. Por exemplo, a esfera e o toro não têm bordo, e nem por isso elas são equivalentes, como veremos mais adiante. |
|
CapIV-pg1 |
|