|
|
CapIII-pg2 |
|
Curvas fechadas no espaço recebem o nome de nós, como os nós de marinheiros, embora nós de marinheiros não sejam fechados (as pontas da corda sempre ficam soltas, aqui elas são emendadas). |
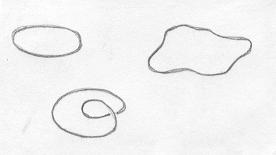
O círculo no espaço é o tipo mais simples de nó, chamado de nó trivial. Na verdade, qualquer deformação de um círculo no espaço é chamada de nó trivial. |

|
Veja agora dois nós que não são triviais: o nó trifólio... |

|
...e o nó figura-oito. |

|
O nó que já mostramos como sendo o bordo de uma superfície pode ser deformado para se transformar no nó trifólio, como mostra a seqüência abaixo. Atenção que também a câmera muda de posição! |
Uma regra importante que deve ser respeitada quando fizermos deformações, seja de curvas como acima seja de superfícies (ou mesmo vizinhanças de pontos na superfície), é não permitir que o objeto que está sendo deformado se auto-intersecte. Ou seja, em nenhum momento é permitido que dois pontos distintos do objeto ocupem o mesmo lugar do espaço. Isso impede, no exemplo acima, que o nó seja transformado no nó trivial. |
Dois nós são ditos equivalentes se um pode ser deformado de forma a se transformar no outro. Por exemplo, o nó que apresentamos como sendo bordo de uma superfície é equivalente ao nó trifólio. Na verdade, podemos até abusar da linguagem, dizendo que esses dois nós são iguais, ou o mesmo nó. Isso porque, do ponto de vista que iremos adotar nesse texto, que é o ponto de vista da área da matemática chamada Topologia, dois objetos só são diferentes se não podem ser transformados um no outro através de deformações. Assim, o nó trifólio pode ser representado de várias formas, dentre as quais as duas que consideramos acima. |
|
CapIII-pg2 |
|